A circular park of radius is situated in a colony. Three boys and are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
None
The correct Answer is:A
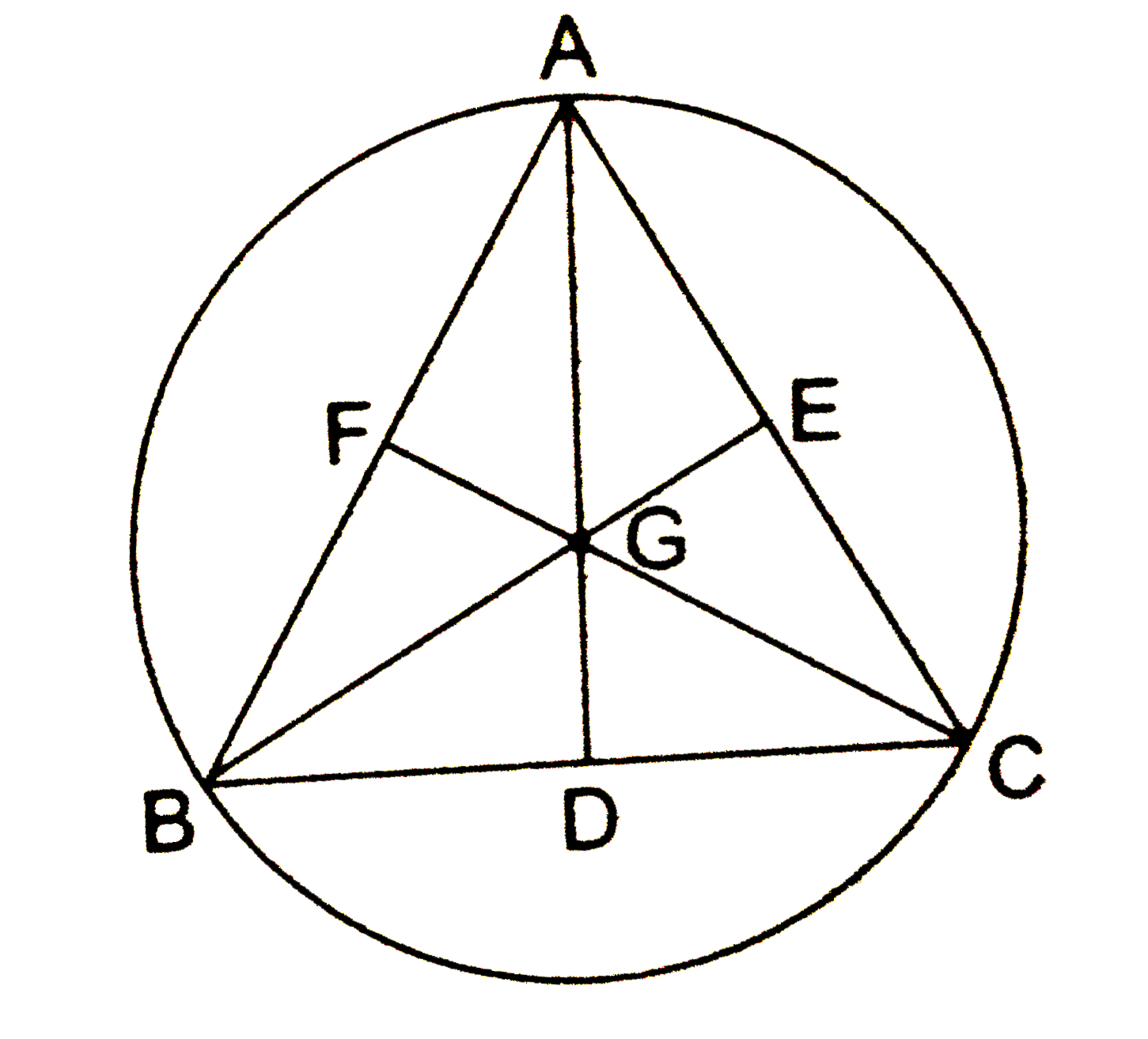
Let and be the posiiton of Ankur, Brijesh and Chirag respectively.
Now,
chord AB chord BC chord CA
is an equilateral triangle.
Let and be the medians of and let be its centroid.
Since, in an equilateral triangle, the centroid coiincides with its circumcentre, we have
Since, the centroid of a triangle divides a median in the ratio ,we have
.
In right , we have
.
.
Hence , the length of each telephone string is m .
Similar Questions
A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk to each other.
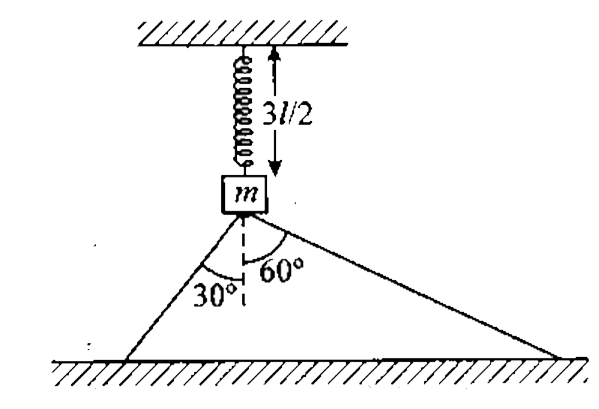
View SolutionFigure-2.107 shows a block of mass m attached to a spring of force constant k and connected to ground by two string of equal lengths making an angle 90∘ with each other. In relaxed state natural length of the spring is l. In the situation shown in figure, find the tensions in the two strings.
View SolutionA horizontal weightless rod of length 3l is suspended on two vertical strings. Two loads of mass m1 and m2 are in equilibrium at equal distance from each other and from the ends of the strings (Fig). Determie the tension T of the left string at the instant when the right string snaps.

View SolutionA magnetic pole of strength qm is placed at a distance of 20 cm from another magnetic pole of triple its strength. If the two poles exert a force of 2.5 g f on each other, find the strength of each pole.
View SolutionDirection: In the following question, a given questions is followed by information in three statements. You have to decide the data in which statement (s) is sufficient to answer the question and mark your answer accordingly.
8 people – A, B, C, D, E, F, G and H are sitting around a circular table at equal distances to each other facing towards centre (not necessarily in the same order), then how many persons are sitting between C and D, if counted from the left of D.
C is sitting second to the left of F. Four persons are sitting between F and D.
A is sitting fourth to the right of D. Two persons are sitting between A and E.
B is sitting third to the right of G.
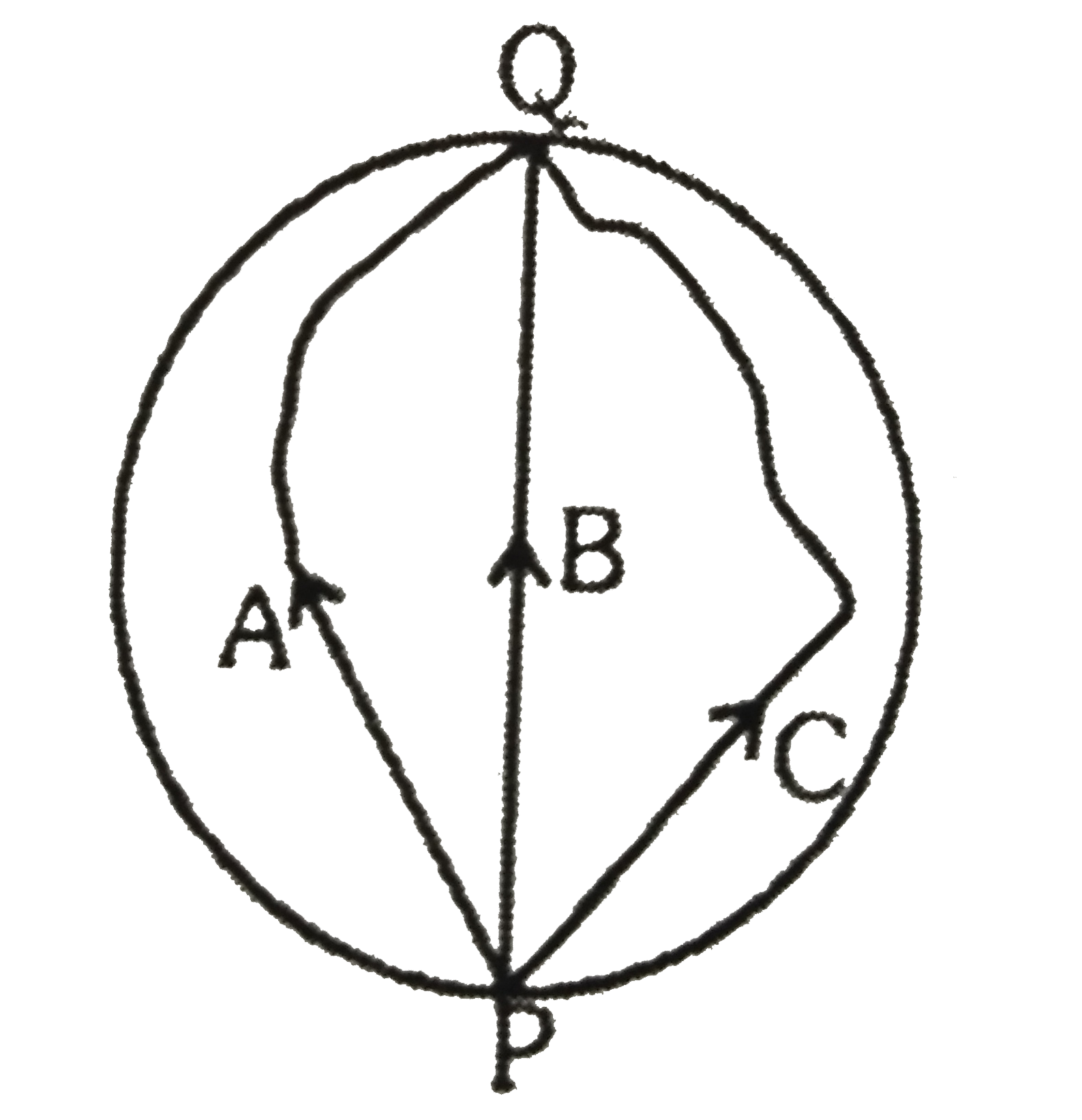
View SolutionThree girls skating on a circular ice ground of radius 200 m start from a point P on the edge of the ground and a point Q diametrically opposite to P following different paths as shown in figure. What is the magnitude of the placement for each ? For which girl is this equal to the actual to the actual length of path skate ?
View SolutionThree thin unifrom circular discs each of mass M and radius R are placed touching each other on a horizontal surface such that an equilateral triangle is formed, when the center of three discs are joined. Find the M.I. about an axis passing through the center of mass system of discs and perpendicular to the plane.
View SolutionTwo identical circular coils of radius 0.1m, each having 20 turns are mounted co-axially 0.1m apart. A current of 0.5A is passed through both of them (i) in the same direction, (ii) in the opposite directions. Find the magnetic field at the centre of each coil.
View SolutionA particle having charge Q and mass M = 2 m is tied to two identical particles, each having mass m and charge q. The strings are of equal length, l each, and they are inextensible. The system is held at rest on a smooth horizontal surface (with string taut) in a position where the strings make an angle of 60∘ between them. From this position the system is released. (a) Find the amplitude of oscillation of M (b) Find maximum speed acquired by M (c) Find tension in the string when all the three particles get in one straight line.
View SolutionThree identical particles, each of mass m, are located in space at the vertices of an equilateral triangle of side length a. They are revolving in a circular orbital under mutual ravitational attraction. Find the speed of each particle. Find the acceleration of the centre of mass of a system comprising of any two particles. Assume that one of the particles suddenly loses its ability to exert gravitational force. Find the velocity of the centre of mass of the system of other two particles after this.
View Solution
