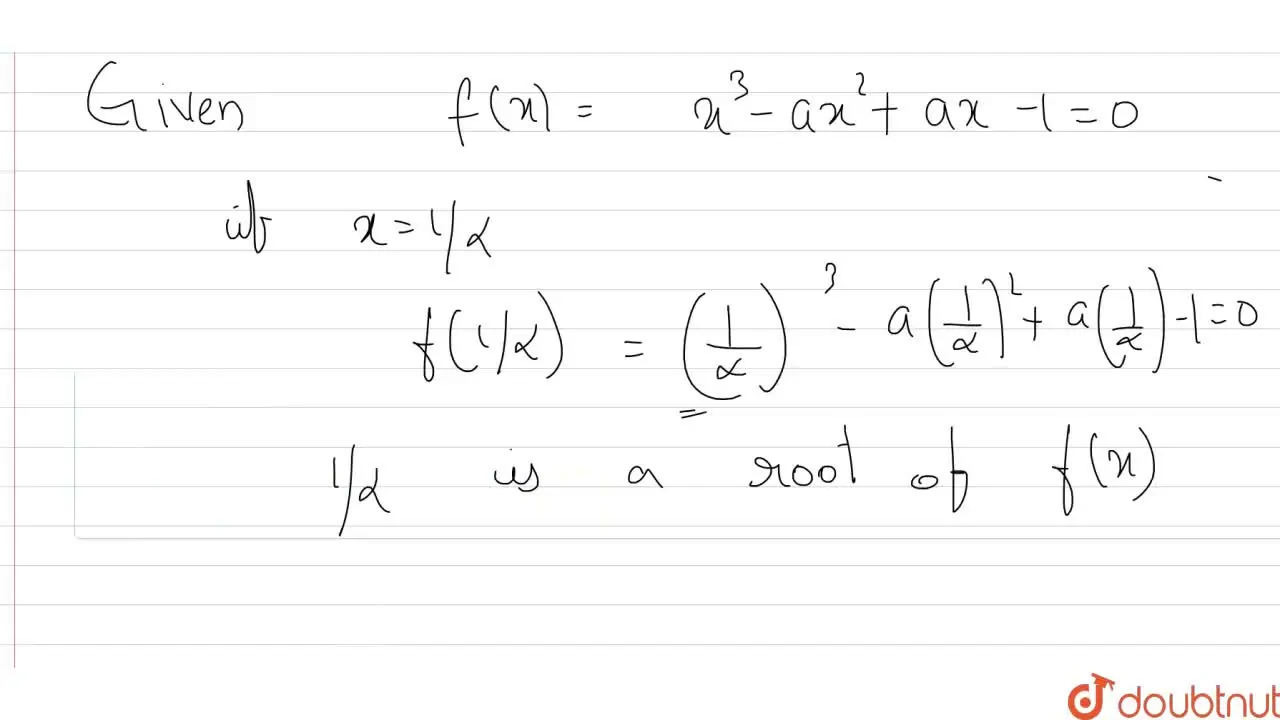Let α≠1 be a real root of the equation x3−ax2+ax−1=0, where a ≠ - 1 is a real number, then a root of this equation, among the following , is : Solution in Telugu
α2
−1α2
1α
1α2
The correct Answer is:C
Step by step video, text & image solution for Let alpha ne 1 be a real root of the equation x^(3) - ax^(2) + ax - 1 = 0, where a ne - 1 is a real number, then a root of this equation, among the following , is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - AAKASH SERIESCHAPTER - THEORY OF EQUATIONSEXERCISE - EXERCISE-III46videos
THEORY OF EQUATIONS
- BOOK - AAKASH SERIESCHAPTER - THEORY OF EQUATIONSEXERCISE - EXERCISE-I47videos
THEORY OF EQUATIONS
- BOOK - AAKASH SERIESCHAPTER - SYSTEM OF CIRCLESEXERCISE - EXERCISE 2.222videos
SYSTEM OF CIRCLES
- BOOK - AAKASH SERIESCHAPTER - TRANSFORMATIONS AND INDENTITIESEXERCISE - PRACTIVE EXERCISE36videos
TRANSFORMATIONS AND INDENTITIES
Similar Questions
The quotient obtained when 3x4−x3+2x2−2x−4 is divided by x2−4 is
02:16View SolutionThe quotient obtained when x4+11x3−44x2+76x+48 is divided by x2−2x+1 is
04:00View SolutionFind the equation of the radical axis of the following circles
x2+y2−3x−4y+5=0,3(x2+y2)−7x+8y−11=004:21View Solutioncos70∘+sin40∘=
02:22View SolutionLet 'a' be a real number. Number of real roots of the equation (x2+ax+1)(3x2+ax−3)=0, is-
02:03View SolutionIf all roots of the equation x^(3)+ax^(2)-ax-1=0 are real and distinct,then the set of values of a is
03:33View SolutionLet αandβ be the roots of the quadratic equation ax2+bx+c=0,c≠0, then form the quadratic equation whose roots are 1−ααand1−ββ.
View Solutionयदि a, b व c वास्तविक संख्याएँ इस प्रकार हों की ac≠0 तो प्रदर्शित करो की समीकरण ax2+bx+c=0 तथा −ax2+bx+c=0 में से कम-से-कम एक समीकरण के मूल वास्तविक होंगे।
04:31View SolutionTwo different real numbers αandβ are the roots of the quadratic equation ax2+c=0a,c≠0, then α3+β3 is:
00:54View SolutionLet α≠1 be a real root of the equation x3−ax2+ax−1=0, where a ≠ - 1 is a real number, then a root of this equation, among the following , is :
View SolutionLet α≠1 be a real root of the equation x3−ax2+ax−1=0, where a≠−1 is a real number. Then, a root of this equation, among the following, is
01:22View SolutionLet αandβ be the roots of the equation x2+ax+1=0,a≠0. Then the equation whose roots are −(α+1β) and −(1α+β) is
03:18View SolutionLet p, p ≠{1,2,3,4}. The number of equations of the form px2+qx+1=0 having real roots is :
01:51View SolutionIf α,β are the roots of the quadratic equation x2+ax+b=0,(b≠0), then the quadratic equation whose roots are α−1β,β−1α is
04:17View SolutionTwo different real numbers αandβ are the roots of the quadratic equation ax2+c=0a,c≠0, then α3+β3 is:
View SolutionLet αandβ be the roots of the equation x2+ax+1=0,a≠0. Then the equation whose roots are −(α+1β) and −(1α+β) is
05:23View Solution