The fraction of the volume of a glass flask must be filled with mercury so that the volume of the empty space may be the same at all temperature is
(αglass=9×10−6/0C,γHg=18.9×10−5/0C)
12
17
14
15
The correct Answer is:B
Step by step video, text & image solution for The fraction of the volume of a glass flask must be filled with mercury so that the volume of the empty space may be the same at all temperature is (alpha_("glass") = 9 xx 10^(-6)//^(0)C, gamma_(Hg) = 18.9 xx 10^(-5) // ^(0)C) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBook:MTG GUIDEChapter:PROPERTIES OF BULK MATTERExercise:AIPMT/NEET (MCQs)
Explore 40 Videos
- PROPERTIES OF BULK MATTERBook:MTG GUIDEChapter:PROPERTIES OF BULK MATTERExercise:NEET Cafe (Topicwise Practice Questions)
Explore 200 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:MTG GUIDEChapter:PHYSICAL WORLD AND MEASUREMENTExercise:AIPMT / NEET MCQ
Explore 14 Videos
- THERMODYNAMICSBook:MTG GUIDEChapter:THERMODYNAMICSExercise:AIPMT/NEET (MCQs)
Explore 26 Videos
Similar Questions
A glass beaker holds exactly 1Lat0∘C
(a) What is its volume at 50∘C ?
(b) If the beaker is filled with mercury at 0∘C, what volume of mercury overflows ehen the temperature is 50∘C ? αg=8.3×10−6per∘C andγHg=1.82×10−4per∘C.
View SolutionA bakelite beacker has volume capacity of 500ccat30∘C. When it is partially filled with Vm volumne (at 30∘C) of mercury, it is found that the unfilled volume of the beaker remains constant as temperature is varied. If γbeaker=6×10−6.∘C−1 and γmercury=1.5×10−4.∘C−1 , where γ is the coefficient of volume expansion , then Vm (in cc) is close to __________.
View Solution
Knowledge Check
A one litre flask contains some mercury. It is found that at different temperatures the volume of air inside the flask remains the same. The volume of mercury in the flask is (αglass=9×10−6/∘C,γHg=180×10−6/∘C)
A150cm3B225cm3C300cm3D450cm3A flask is filled with mercury at temperature 28∘C . If the flask and the contents are heated to 48∘C , the volume of mercury above the mark will be (αglass=9×10−6/∘C , γHg=180×10−6/∘C)
A0.15cm3B0.25cm3C0.3cm3D0.5cm3A two litre glass flask contains some mercury. It is found that at all temperatures the volume of the air inside the flask remains the same. The volume of the mercury inside the flask is (αfor glass =9×10−6/∘C,γ for mercury 1.8×10−4/∘C)
A1500 ccB150 ccC3000 ccD300 cc
In design of a compensated pendulum, a light metal rod of length L0 = 1.0 m is attached to a glass tube filled with mercury. Neglecting the mass of the glass tube as well, calculate the height of mercury column in the glass tube so that centre of mass of this system does not rise or fall with temperature Given : λ)Hg)=1.82×10−4K−1,αglass')=9xx10^(-6),alpha_(mηl=1.2×10−5K−1
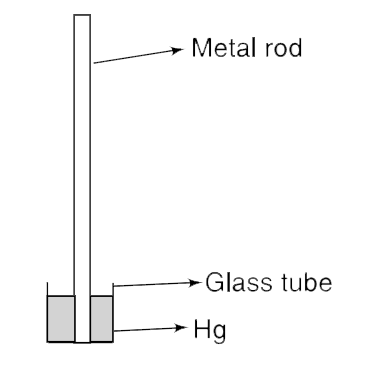
View Solutiona glass tube of length 133cm and of uniform cross-section is to be filled with mercury so that the volume of the unoccupied by mercury remains the same at all temperatures. If cubical coefficient for glass and mercury are respectively 0.000026/∘C and 0.000182/∘C , calculate the length of mercury column.
View SolutionA glass tube is attached to the bottom of a thin iron rod of length 1m. To what height must the glass tube be filled with mercury so that the centre of mass of the pendulum formed will not rise or all with changes in temperature?
(Linear expansivity of glass =9×10−6K−1, that of iron =12x10−6K−1 and cubical edxpansivity of mercury =18.2×10−5K−1)
View SolutionA glass tube of length l0 and of uniform cross-section is to be filled with mercury so that the length of the tube unoccoupied by mercury remains same at all temperatures. If γg=3α , calculate length of mercury column.
View SolutionA glass flask of volume 200cm3 is just filled with mercury at 20∘C. The amount of mercury that will overflow when the temperature of the system is raised to 100∘C is (γglass=1.2×10−5/C∘,γmercury=1.8×10−4/C∘)
View Solution

