A projectile is projected with the initial velocity (6i+8j)m/s. The horizontal range is (g=10m/s2)
4.8 m
9.6 m
19.2 m
14.0 m
The correct Answer is:B
Here, ucosθ=6,usinθ=8andg=10ms−2
∴R=u2sin2θg=2u2sinθcosθg=2(usinθ)(ucosθ)g
=2×8×610=9.6m
Topper's Solved these Questions
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (UNIFORM CIRCULAR MOTION)
8 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - CHECK YOUR NEET VITALS
22 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (MOTION IN A PLANE )
23 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - AIPMT/NEET MCQS
32 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
Similar Questions
What are the two angles of projection of a projectile projected with velocity of 30m/s, so that the horizontal range is 45m. Take, g=10m/s2.
View SolutionWhat are the angles of projection of a projectile projected with velocity 30ms−1, so that the horizontal range is 45 m ? Take g=10ms−2.
View Solution
Knowledge Check
A body is projected with a initial velocity of (8ˆi+6ˆj)ms−1 . The horizontal range is (g=10ms−2)
A9.6 mB14 mC50 mD100 mA projectile is thrown with an initial velocity of (x→i+y→j)m/s . If the range of the projectile is double the maximum height reached by it, then
Ax−2yBy=2xCx=yDy=4xA particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
A10mB5mC2.5mD1m
A particle is projected with velocity 20√2m/s at 45∘ with horizontal. After 1s(g=10m/s2) match the following table
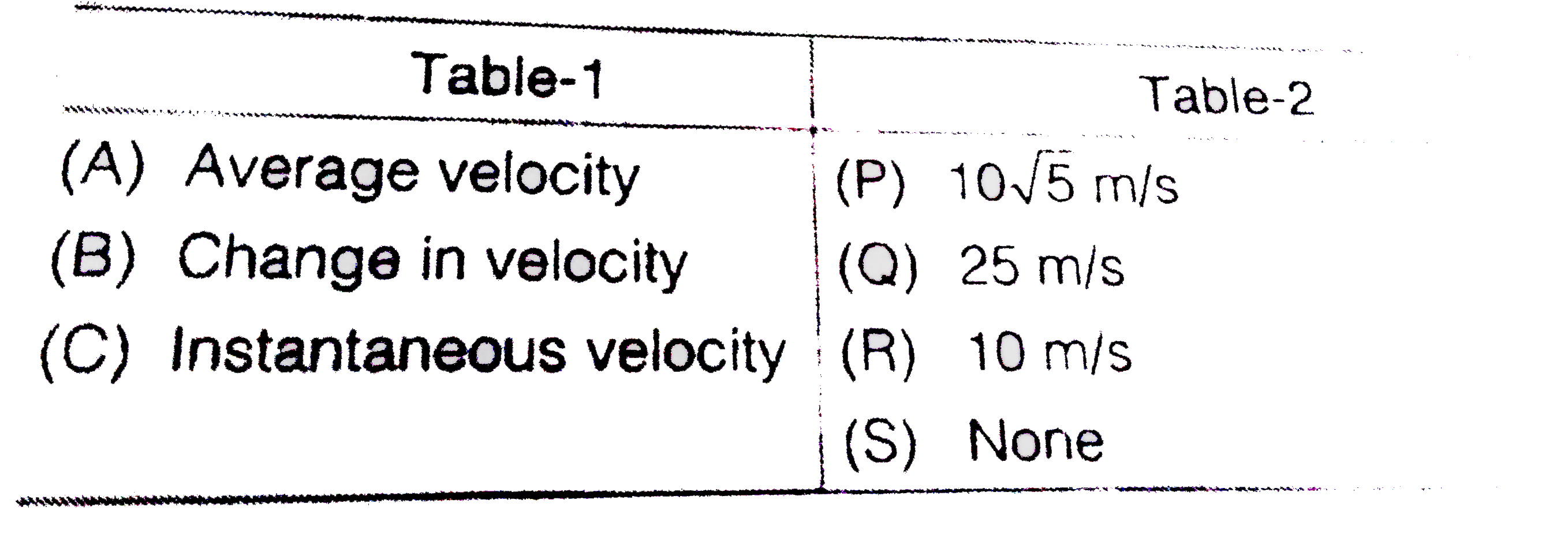
View SolutionA projectile is projected from top of a wall 20m height with a speed of 10m/s horizontally. Find range (g=10ms2)
View SolutionA projectile is projected with initial velocity (6ˆi+8ˆj) m/s.Minimum time after which its velocity becomes parallel to the line 4y-3x+2=0, is ?(¯g=−10ˆjm/s2)
View SolutionA projectile is projected in air with initial velocity →v=(3ˆi+4ˆj) m/s from the origin. The equation of trajectory of the projectile is given as (g=−10ˆjms2) (neglect air resistance )
View SolutionA projectile is projected from ground with an initial velocity (5ˆi+10ˆj)m/s If the range of projectile is R m, time of flight is Ts and maximum height attained above ground is Hm, find the numerical value of R×HT. [Take g=10m/s2]
View Solution
