An astronaout is rotating in a rotor of radius 4m. If he can withstand upto acc. Of 10g, then what is the maximum number of permissible revolutions? (g=10m/s2)
In case of uniforin circular motion
ar=v2r=ω2r [as v=rω ]
or ar=(2πv)2r [As ω=2πv ]
υ=12π√arr
Hence ar<10g, so
υ<12√10×104 i.e υmax=[52π] rev/sec
Topper's Solved these Questions
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (DISTANCE AND DISPLACEMENT)
2 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (SPEED AND VELOCITY)
9 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - AIPMT/NEET MCQS
32 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
Similar Questions
A spaceman in training is rotated in a seat at the end of a horizontal arm of length 5 m. If he can with stand acceleration upto 9 g, then what is the maximum number of revolution per second permissible? (Take, g =10ms−2)
View SolutionIn the diamram shown in figure , match the following (g=10m/s2)

View Solution
Knowledge Check
If a speed man is rotated at the end of a long beam of length 5m and the acceleration of 9g, then the number of revolution performed will be
(g=10m/s2)A3√2πrpsB3π√2rpsC2√53rpsD√33πrpsA body of mass 1 kg is rotating in a verticle circle of radius 1 m .What will be the difference in its kinetic energy at the top and bottom of the circle ?
(g=10m/s2)A10 jB20 jC30 jD50 jAn object of mass 2 kg is whirled rround in a verticle circle of radius 1m with a constant speed of 4m/s .Then the maximum tension in the string is (g=10m/s2)
A32 NB52 NC72 ND92 N
Tension in the rope at the rigid support is (g=10m/s2)
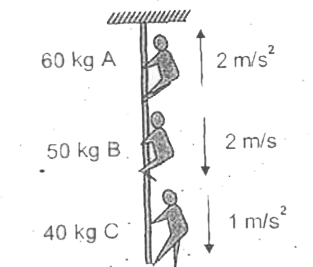
View SolutionIn the diagram shown in fifure ,match the following (g=10m/s2)
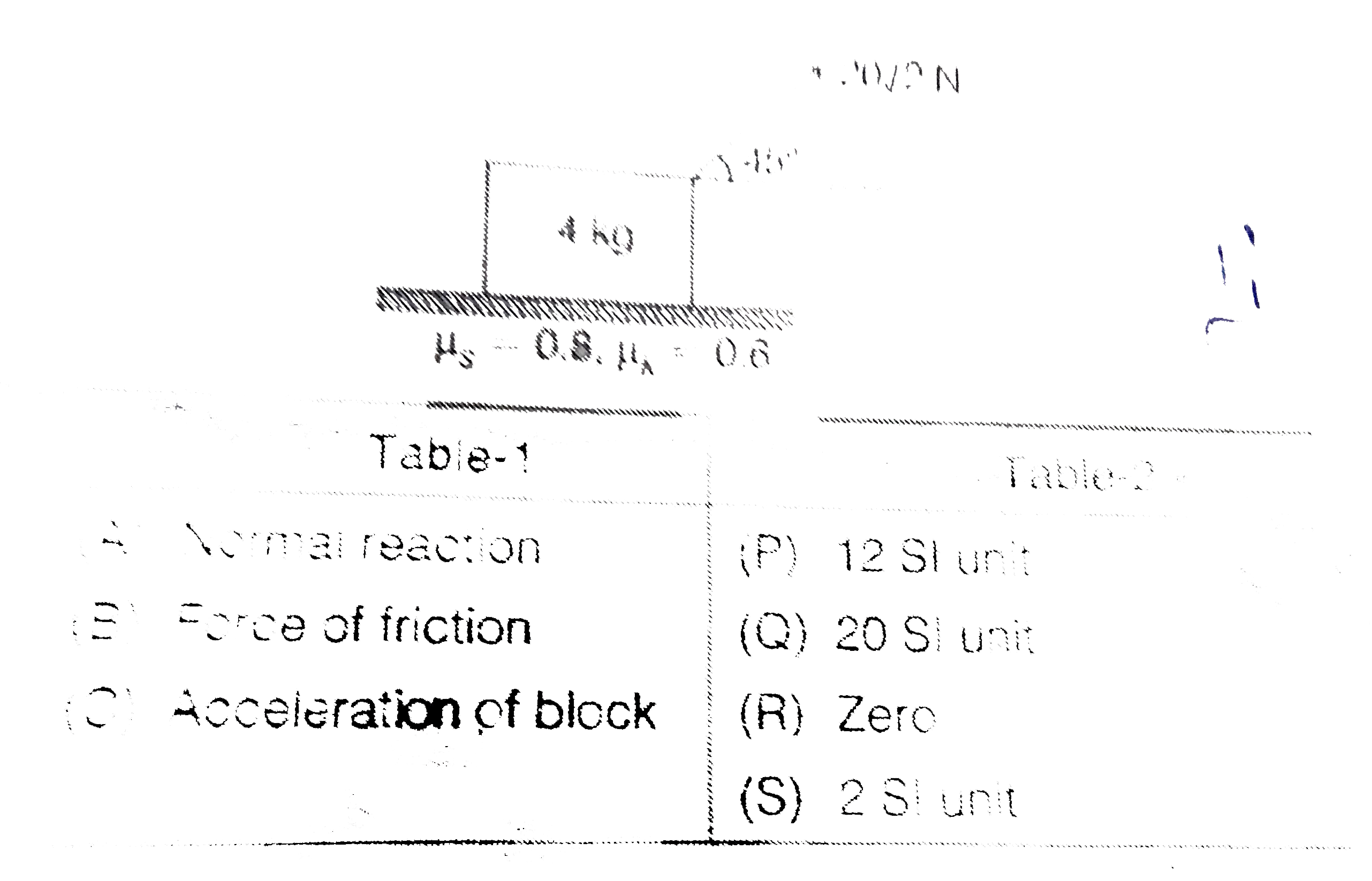
View SolutionA body of mass 40 kg wants to climb up a rope hanging vertically. The rope can withstands a maximum tension of 500 N. What is the maximum acceleration with which the boy can climb rope? Tak e g=10m/s2
View SolutionIn the arrangement as shown, tension T2 is -
(g=10m/s2)
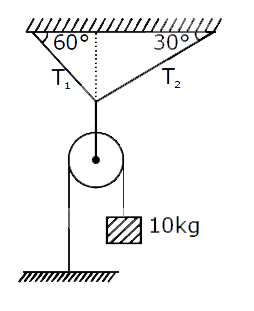
View SolutionWhat is the angle of banking of a railway track of radius of curvature 250m, if the maximum velocity of the train is 90 km / hr .? ( useg=10ms2)
View Solution
