Motion of a particle is defined by m. Graphically represent the variation of velocity with time.
To solve the problem of finding the variation of velocity with time for the motion of a particle defined by the equation x=3−4t+5t2, we will follow these steps:
Step 1: Differentiate the position function to find velocity
The position of the particle is given by:
x(t)=3−4t+5t2
To find the velocity v(t), we differentiate x(t) with respect to time t:
v(t)=dxdt=ddt(3−4t+5t2)
Step 2: Apply the differentiation
Using the rules of differentiation:
- The derivative of a constant (3) is 0.
- The derivative of −4t is −4.
- The derivative of 5t2 is 10t.
Thus, we have:
v(t)=0−4+10t=10t−4
Step 3: Determine the velocity at specific time points
Now, we can calculate the velocity at specific time points to understand its variation:
- For t=0:
v(0)=10(0)−4=−4m/s
- For t=0.2 seconds (which is 210):
v(210)=10(210)−4=2−4=−2m/s
- For t=0.4 seconds:
v(0.4)=10(0.4)−4=4−4=0m/s
- For t=0.6 seconds:
v(0.6)=10(0.6)−4=6−4=2m/s
- For t=1 second:
v(1)=10(1)−4=10−4=6m/s
Step 4: Create a table of values
We can summarize the values in a table:
| Time (s) | Velocity (m/s) |
|----------|----------------|
| 0 | -4 |
| 0.2 | -2 |
| 0.4 | 0 |
| 0.6 | 2 |
| 1 | 6 |
Step 5: Plot the graph
Now, we can plot the graph of velocity v(t) against time t:
- The x-axis represents time (in seconds).
- The y-axis represents velocity (in m/s).
The points we calculated will help us plot the graph:
- At t=0, v=−4
- At t=0.2, v=−2
- At t=0.4, v=0
- At t=0.6, v=2
- At t=1, v=6
By connecting these points, we will see a straight line that starts below the x-axis and crosses it at t=0.4 seconds, indicating that the velocity changes from negative to positive.
Conclusion
The graph represents the variation of velocity with time, showing that the particle starts with a negative velocity, reaches zero, and then increases positively.
---
The position of the particle is given by:
x(t)=3−4t+5t2
To find the velocity v(t), we differentiate x(t) with respect to time t:
v(t)=dxdt=ddt(3−4t+5t2)
Using the rules of differentiation:
- The derivative of a constant (3) is 0.
- The derivative of −4t is −4.
- The derivative of 5t2 is 10t.
v(t)=0−4+10t=10t−4
Now, we can calculate the velocity at specific time points to understand its variation:
- For t=0:
v(0)=10(0)−4=−4m/s
- For t=0.2 seconds (which is 210):
v(210)=10(210)−4=2−4=−2m/s
- For t=0.4 seconds:
v(0.4)=10(0.4)−4=4−4=0m/s
- For t=0.6 seconds:
v(0.6)=10(0.6)−4=6−4=2m/s
- For t=1 second:
v(1)=10(1)−4=10−4=6m/s
We can summarize the values in a table:
|----------|----------------|
| 0 | -4 |
| 0.2 | -2 |
| 0.4 | 0 |
| 0.6 | 2 |
| 1 | 6 |
Now, we can plot the graph of velocity v(t) against time t:
- The x-axis represents time (in seconds).
- The y-axis represents velocity (in m/s).
- At t=0, v=−4
- At t=0.2, v=−2
- At t=0.4, v=0
- At t=0.6, v=2
- At t=1, v=6
The graph represents the variation of velocity with time, showing that the particle starts with a negative velocity, reaches zero, and then increases positively.
Topper's Solved these Questions
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (DISTANCE AND DISPLACEMENT)
2 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (SPEED AND VELOCITY)
9 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - AIPMT/NEET MCQS
32 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
Similar Questions
The position of a particle is given by x=7+3t3 m and y=13+5t−9t2m, where x and y are the position coordinates, and t is the time in s. Find the speed (magnitude of the velocity) when the x component of the acceleration is 36m/s2.
View SolutionThe velocity time relation of a particle is given by v =(3t2−2t−1)m/s Calculate the position and acceleration of the particle when velocity of the particle is zero . Given the initial position of the particle is 5m .
View Solution
Knowledge Check
The motion of a particle is described as s=2−3t+4t3. What is the acceleration of the particle at the point where its velocity is zero?
AA)0BB)4CC)8 unitDD)12 unitFigure shows the position the graph for a particle in one dimensional motion. Which of the graphs in fugure represent the variation in the velocity of the particle with time ?
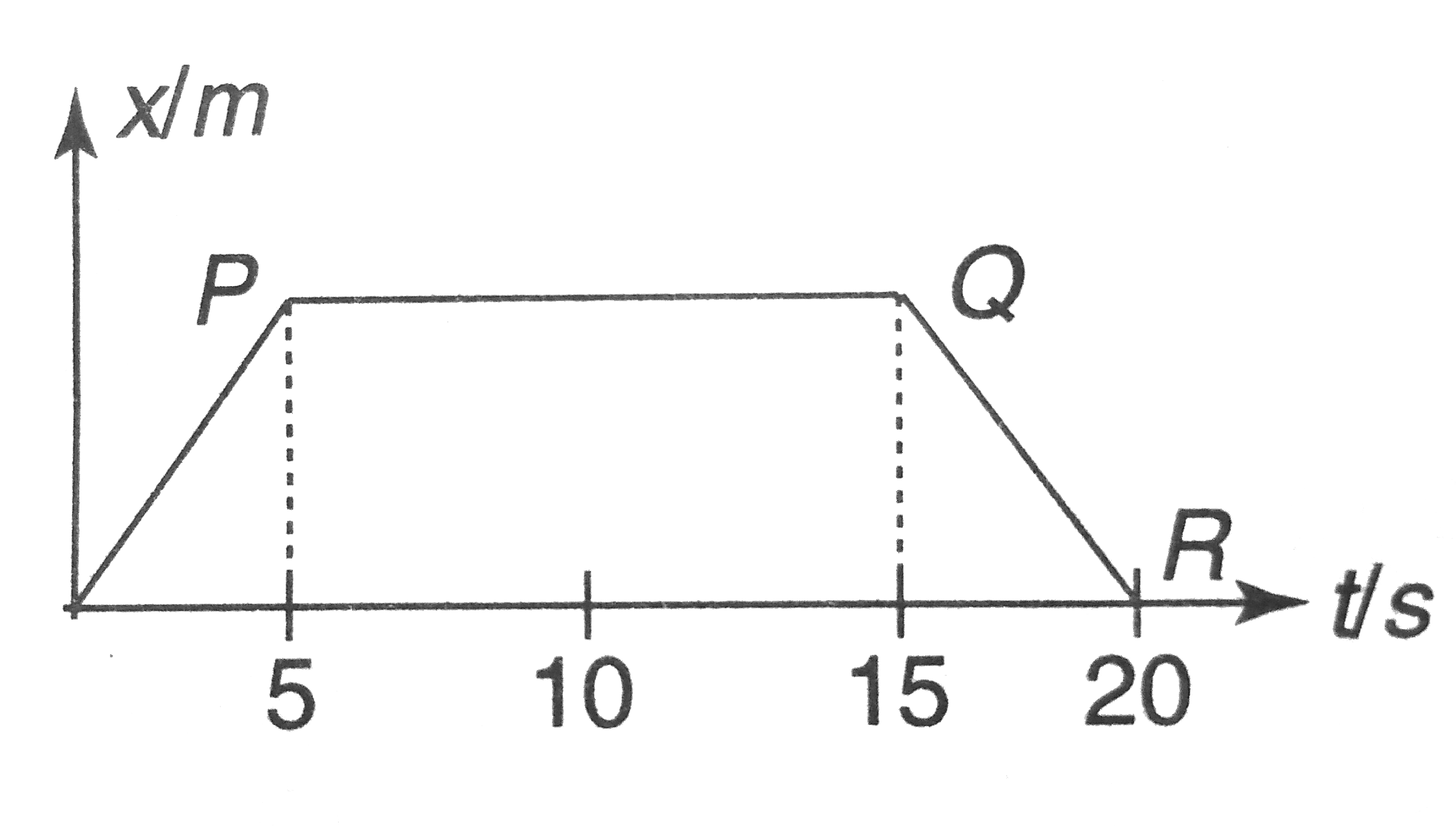 A
A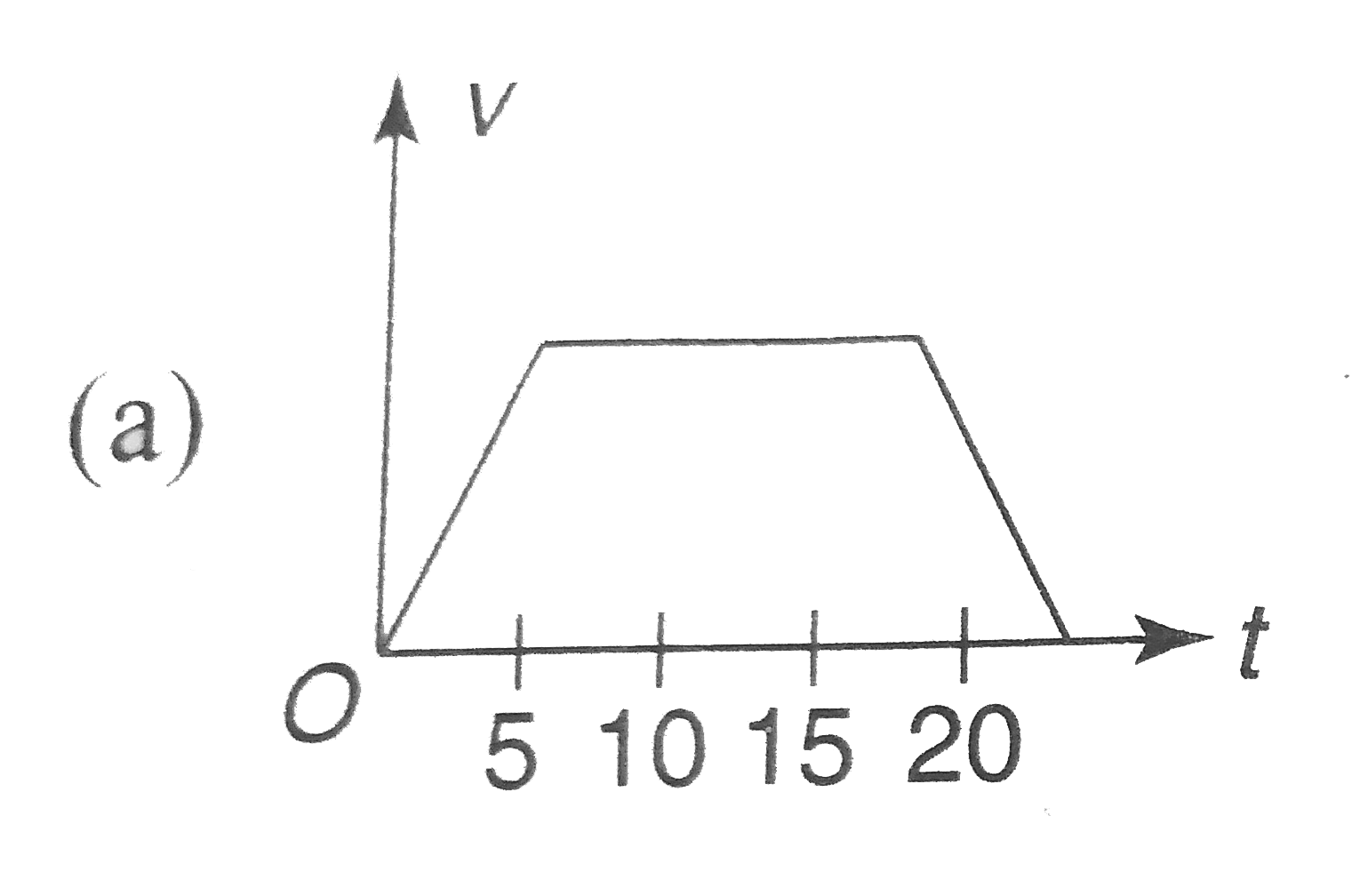 .B
.B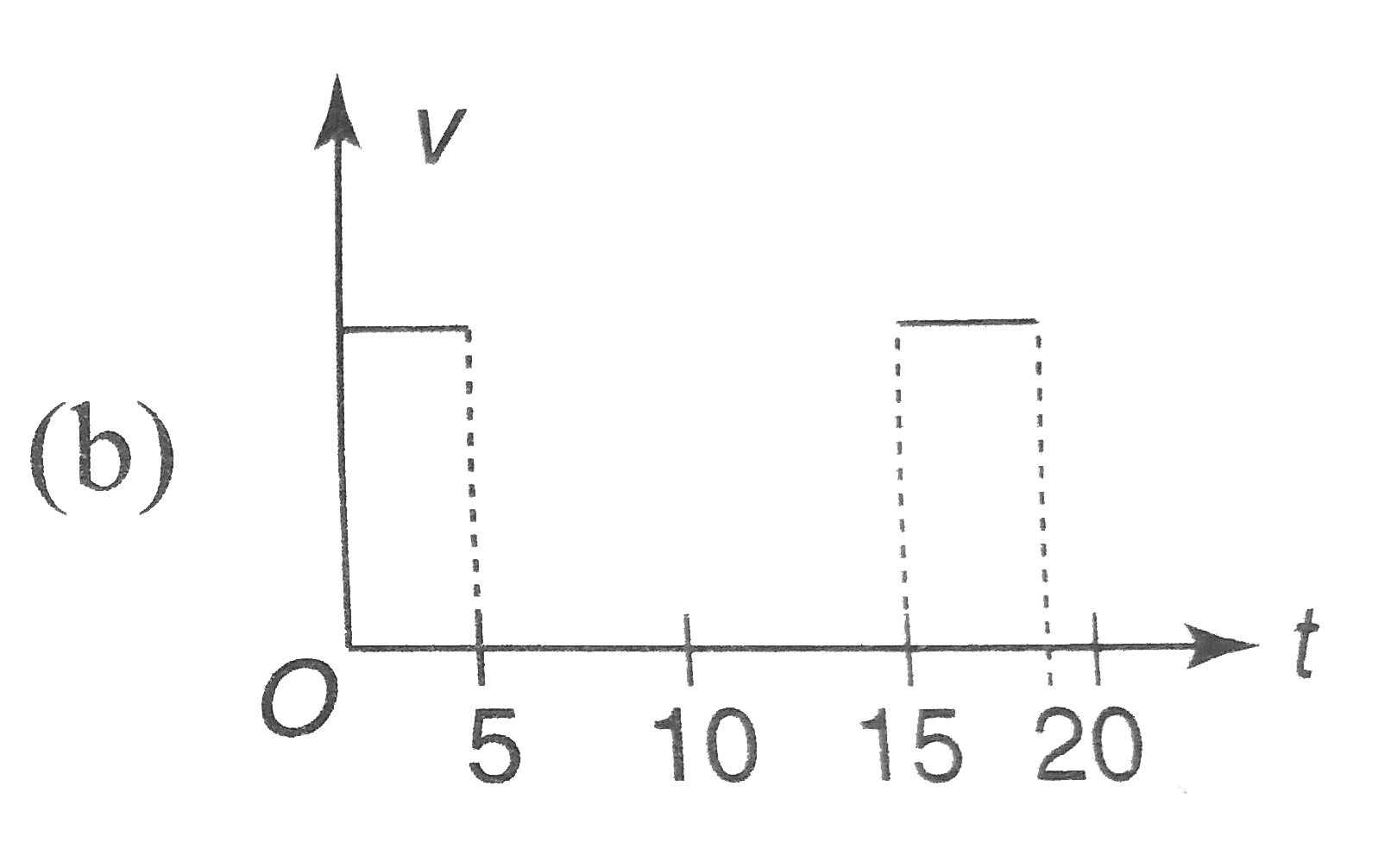 .C
.C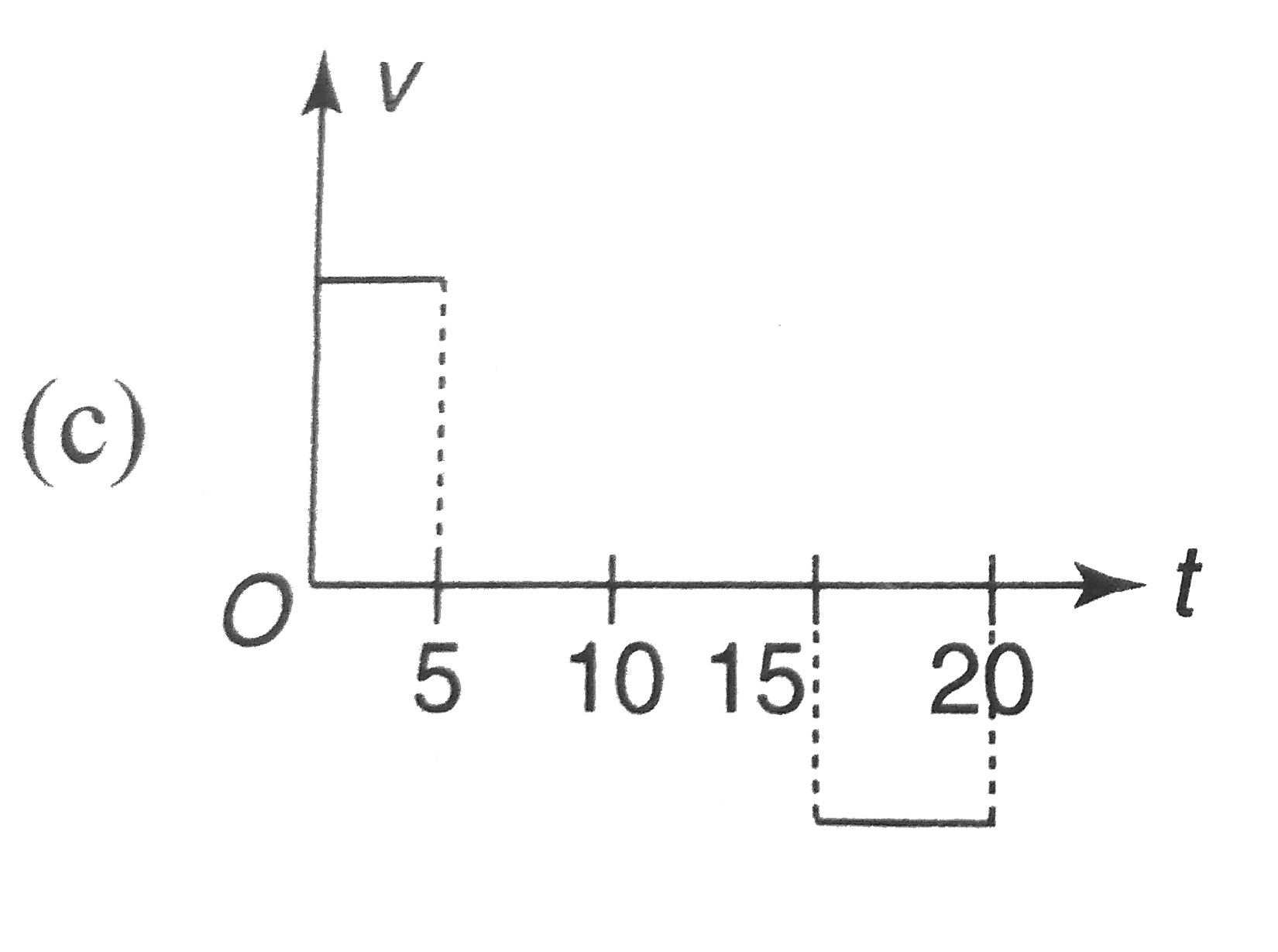 .D
.D .
.Variation of displacement x is described by equation x=3−4−5t2−6t3 in terms of time t. The initial velocity along the axis is denoted by
A3 unitsB−4 unitsC−5 unitsD−6 units
The positione of a particle is expressed as →r=(4t2ˆi+2tˆj) m, where t is time in second. Find the velocity o the particle at t = 3 s
View SolutionThe motion of a particle is described as S=2−3t+4t3 what is the acceleration of the paricle at the point where its velocity is zero ?
View SolutionDisplacement (x) of a particle is related to time (t) as
x=at+bt2−ct3
where a,b and c are constant of the motion. The velocity of the particle when its acceleration is zero is given by:
View SolutionThe velocity of the particle at any time t is given by vu=2t(3−t)ms−1. At what time is its velocity maximum?
View SolutionThe displacement of a particle at time t is given by s=2t3−5t2+4t−3 . The time when the acceleration is 14ft/ sec2 is
View Solution
