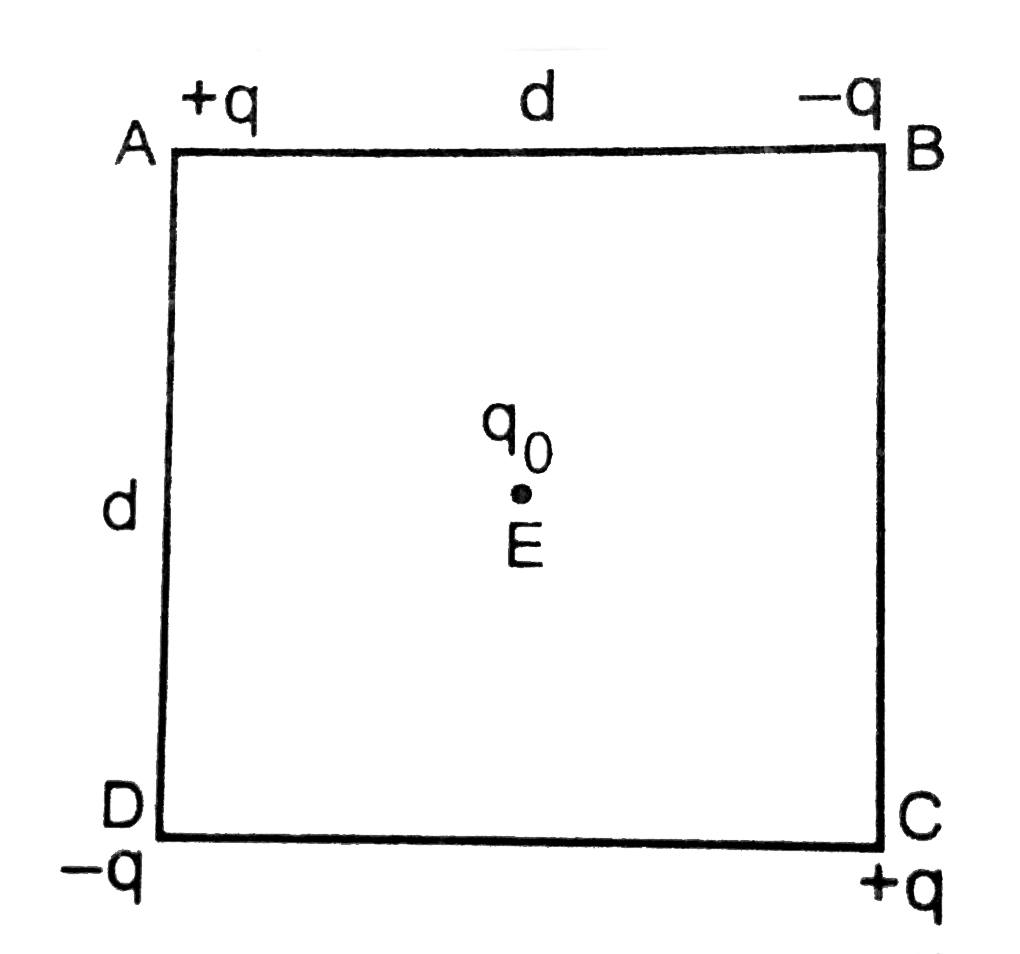
Four charges are arranged at the corners of a square ABCD of side d as show in figure.
(a) Find the work required to put together this arrangement.
(b) A charge q0 is brought to the centre E of the square the four charges being held fixed at its corners. How much extra work is needed to do this ?
 Solution in Gujrati
Solution in Gujrati
Suppose sides of square ABCD are AB = BC =CD= DA = d. Hence AC= BD=d √2
(i) Work needed to bring charge +q to A when no charge is present on square is W1=0
(ii) Work needed to bring -q to B when +q is at A
W2=kq(−q)AB=−kq2d
(iii) Now work needed to bring charge +q to C when +q is at A and -q is at B
W3=k(+q)(+q)AC+(k−q)(+q)BC
∴W3=kq2d√2−kq2d
(iv) Now work done to bring -q to D when +q is at A ,-q at B and +q at C ,
W4=K(+q)(−q)AD+k(−q)(−q)BD+k(+q)(−q)CD
W4=−kq2d+kq2d√2−kq2d
Hence, work done to bring given charge on square,
W=W1+W2+W3+W4
∴W=0−kq2d+kq2d√2−kq2d+kq2d√2−kq2d
=−4kq2d+2kq2d√2
=−kq2d[4−√2]
W=−q24π∈0d[4−√2]
Hence, the work done depends only on the arrangement of the charges.
(b) E is the centre of square ABCD. Suppose, r is the distance of every vertex and hence
r=d√2 . If V is the potential at E .
V=k(+q)d/√2+k(−q)d/√2+k(+q)d/√2+k(−q)d/√2
∴V=0
∴ The work done to bring charge q0 at the point E
W=q0×V
=q0×0
∴W=0
Hence, no work is required to bring any charge to the centre of square. But, not on how they are brought to square vertices.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B ( Numerical From Textual Exercise )
46 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B ( Numerical From DARPAN. Based on Textbook )
19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ( Section -A) Try Yourself
50 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
5 Videos
- MAGNETISM AND MATTERBOOK - KUMAR PRAKASHANCHAPTER - MAGNETISM AND MATTEREXERCISE - SECTION D Multiple Choice Questions (MCQs) (MCQs asked in Competitive Exams) MCQs asked in Board Exam and GUJCET
7 Videos
Similar Questions
Two charge 5×10−8C and −3×10−8 C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero ? Take the potential at infinity to be zero.
View SolutionAn electric field is represented by →E=Axˆi where A = 10Vm2 . Find the potential of the origin with respect to the point (10,20) m.
View SolutionWhat are conservative force , non - conservative force , conservative field and non - conservative field ?
View SolutionDetermine the current in each branch of the given network.

View SolutionAt a place on earth the vertical component of earth's magnetic field is √3 times its horizontal component. The angle of dip at this place is …...
View SolutionFour charges are arranged at the corners of a square ABCD, as shown in the adjoining figure, The force on a positive charge kept at the centre O is
View SolutionFour charges are arranged at the corners of a square ABCD pf side d, as shown in Fig. Find the work required to put together this arrangement (b) A charge q0 brought to the center E of the square, the four charges being held fixed at the corners . How much extra work in needed to do this ?
View SolutionFour charges are arranged at the corners of a square ABCD as shown in the figure. The force on the charge kept at the centre O will be:
View SolutionFour charges are arranged at the corners of a square ABCD, as shown. The force on a positive charge kept at the centre of the square is

View Solutionचित्र 2.15 में दर्शाए अनुशार चार आवेश भुजा d वाले किसी वर्ग ABCD के शीर्षों पर व्यवस्थित किए गए हैं। (a) इस व्यवस्था को एक साथ बनाने में किया गया कार्य ज्ञात कीजिए । (b) कोई आवेश q0 वर्ग के केंद्र E पर लाया जाता है तथा चारों आवेश अपने शीर्षों पर दृढ़ रहते हैं । ऐसा करने के लिए कितना अतिरिक्त कार्य करना पड़ता है ?
View SolutionFour charges are arranged at the corners of a square ABCD of side d. as shown in fig. Find the work required to put together this arrangement. (b) A charge q0 is brought to the centre of the square, the four being held fixed at its corners. How much extra work is needed to do this ?
View Solutionचित्र में दर्शाए अनुसार चार आवेश d भुजा वाले किसी वर्ग ABCD के शीर्षों पर व्यवस्थित किए गए है । (a). इस व्यवस्था को एक साथ बनाने में किया गया कार्य ज्ञात कीजिए (b) कोई आवेश q0 वर्ग के केंद्र E पर लाया जाता है तथा चारों आवेश अपने शीर्षों पर दृढ़ रहते हैं। ऐसा करने के लिए कितना अतिरिक्त कार्य करना पड़ता है?
View SolutionFour charges are arranged at the corners of a square ABCD as shown in the figure. The force on the charge kept at the centre O will be:

View SolutionFour charges are arranged at the corners of the square PQRS of side a as shown in the figure . (a) Find the work required to assemble these charges in the given configuration . (b) Suppose a charge q is brought to the center of the square by keeping the four charges fixed at the corners how much extra work is required for this ?
View SolutionFour charges are arranged at the comers of a square ABCD of side d, as shown in Fig.
a. Find the work required to put together this arrangement
b. A charge q0 is brought to the centre E of the square, the four charges being held fixed at its corners. How much extra work is needed to do this?n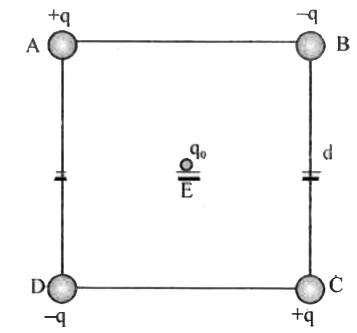
View Solution
