Derive the formula for the electric potential due to an electric dipole at a point from it. Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

A dipole is placed with origin at its midpoint. Its charge -q and +q is separated by a distance 2a. The magnitude of a dipole moment of the dipole is p= 2aq and its direction is from -q to +q.
Let point P away from the midpoint of dipole and $r_{1}$ and $r_{2}$ are the distance of P from +q and q respectively which is shown in the figure .

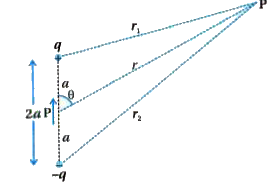
The potential due to the charge +q at point P is
$V_{1} \frac{k (+ q)}{r_{1}}$ and
The potential due to the charge -q,
$V_{2} = \frac{k (- q)}{r_{2}} = \frac{k q}{r_{2}}$
According to superposition principle, the total potential at point P
$V = V_{1} + V_{2}$
$= \frac{k q}{r_{1}} - \frac{k q}{r_{2}}$
$= k q [\frac{1}{r_{1}} - \frac{1}{r_{2}}]$
Draw qN $⊥$ OP In $Δ q O N ∠ q O N = θ$
$∴ O N = r - r_{1}$
and $cos θ = \frac{O N}{O q} \Rightarrow O N = Q q cos θ$
$∴ r - r_{1} = a cos θ \Rightarrow r_{1} = r - a cos θ$
$= r (1 - \frac{a_{r 1}}{r} cos θ)$
$\Rightarrow r_{1}^{2} = r^{2} {(1 - \frac{a}{r} cos θ)}^{2}$
$= r^{2} (1 - \frac{2 a cos θ}{r} + \frac{a^{2}}{r^{2}} {cos}^{2} θ)$
$= r^{2} (1 - \frac{2 a cos θ}{r})$
Putting $r > > a \Rightarrow \frac{a^{2}}{r^{2}} = 0$
and draw OM $⊥$ (-qp=P) then in $Δ -$ qOM P(-q) M $= θ$ and (-q) M $= r_{2} - r$
$∴ cos θ \frac{(- q) M}{O - (- q)} \Rightarrow (- q) M = m O (- q) cos θ$
$∴ r_{2} - r = a cos θ$
$: > r_{2} = r + a cos θ$
$∴ r_{2} = r (1 + \frac{a}{r} cos θ)$
Similarly $r_{2}^{2} = r^{2} (1 + \frac{2 a cos θ}{r})$
Now from equation (4 )
$∴ \frac{1}{r_{1}} = \frac{1}{r} {(1 - \frac{2 a cos θ}{r})}^{- 1 / 2}$
$= \frac{1}{r} (1 + \frac{a cos θ}{r})$
only two terms be taken from expansion and,
$\frac{1}{r_{2}} = \frac{1}{r} (1 - \frac{a cos θ}{r})$
Now from equation (5)
only two terms be taken from expansion .
$\Rightarrow$ Putting the values of equation (6) and (7) in equation (1) ,
$V = \frac{k q}{r} [(1 + \frac{a cos θ}{r}) - (1 - \frac{a cos θ}{r})]$
$= \frac{k q}{r} [\frac{2 a cos θ}{r}]$
$= \frac{k (p) cos θ}{r^{2}} [∵ 2 a q = p]$
$= \frac{k \to P . \to r}{r^{2}} [∵ p cos θ = \to P . ˆ r]$
$∴ V = \frac{p . ˆ r}{4 π \in_{0} r^{2}} or \frac{p cos θ}{4 π \in_{0} r^{2}} or \frac{k p cos θ}{r^{2}}$
Hence potential due to a point charge decreases according $\frac{1}{r}$ and potential due to a dipole decreases according to $\frac{1}{r^{2}}$ distance . The molecular dipoles are very small and such an approximation is very well applicable to them.

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-ELECTROSTATIC POTENTIAL AND CAPACITANCE-Section D ( MCQs asked in Cometitive Exams )

Home
Ask Doubt
Profile