If mandσ2 are the mean and variance of the random variable X, whose distribution is given by:
X=x:0123P(X=x):1312016 Solution in Telugu
m=σ2=2
m=1,σ2=2
m=σ2=1
m=2,σ2=1
The correct Answer is:C
Step by step video, text & image solution for If m and sigma^(2) are the mean and variance of the random variable X, whose distribution is given by: {:(X=x:,0,1,2,3),(P(X=x):,(1)/(3),(1)/(2),0,(1)/(6)):} by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RANDOM VARIABLE Book:AAKASH SERIESChapter:RANDOM VARIABLE Exercise:EXERCISE - II
Explore 76 Videos
- RANDOM VARIABLE Book:AAKASH SERIESChapter:RANDOM VARIABLE Exercise:PRACTICE EXERCISE
Explore 34 Videos
- RANDOM VARIABLE Book:AAKASH SERIESChapter:RANDOM VARIABLE Exercise:ADDITIONAL EXERCISE
Explore 25 Videos
- QUADRATIC EQUATIONS & EXPRESSIONSBook:AAKASH SERIESChapter:QUADRATIC EQUATIONS & EXPRESSIONSExercise:PRACTICE EXERCISE
Explore 88 Videos
- RANDOM VARIABLESBook:AAKASH SERIESChapter:RANDOM VARIABLESExercise:Exercise 4.4
Explore 9 Videos
Similar Questions
A person who tosses an unbiased coin gains two points for turning up a head and loses one point for a tail. If three coins are tossed and the total score X is observed, then the range of X is
View SolutionA random variable X ahs the following distribution
x1234P(X=x)c2c3c4c
The value of c is
View SolutionThe probability function of a random variable X is given by
p(x)=13, if x = -1, 0, 1
=0, otherwise.
Find the distribution function of X.
View SolutionIf 3x+22x+3=4x+33x+4, then x =
View SolutionA random variable X takes four values with probabilities 1+3x4,(1−x),1+2x4 and 1−4x4. Find the set of values of x for the variable X to have probability distribution.
View SolutionThe mean and variance of a random variable X having a binomial distribution are 4and2 respectively. The P(X=1) is
View SolutionIf m and σ2 are the mean and variance of the random variable X whose distribution is given by
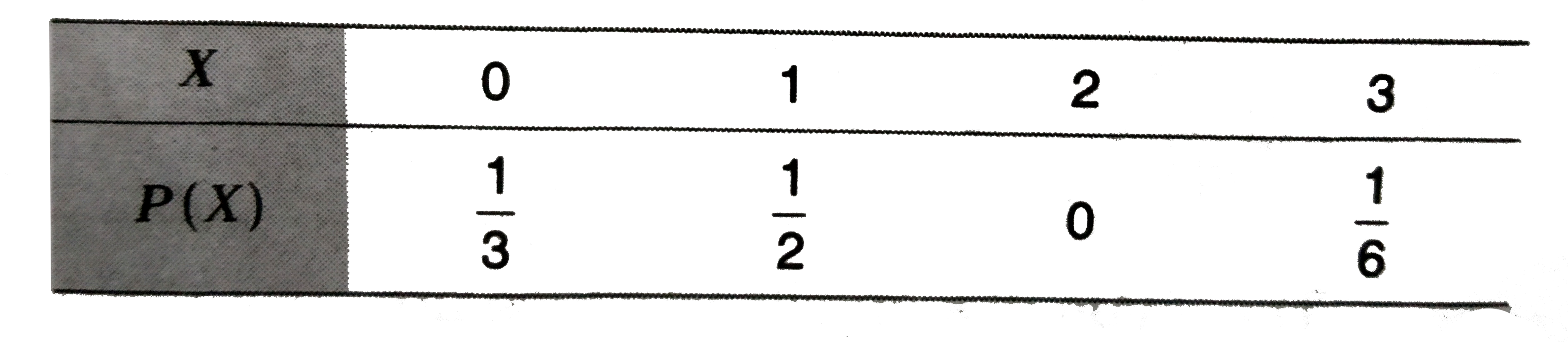
View SolutionThe probability distribution of a random variable X is given below:
X=x0123P(X=x)110210310410
Then the variance of X is
View SolutionIf mandσ2 are the mean and variance of the random variable X, whose distribution is given by:
X=x:0123P(X=x):1312016
View SolutionThe mean and variance of a random variable X having a binomial distribution are 4 and 2 respectively, then P(X=1) is
Theoretical Distributions
View SolutionIf a random variable X has a Poisson distribution such that P(X=1)=P(X=2) then
I: its mean is 2 II: its variance is 1
View SolutionIf a random variable X has a poisson distribution such that P(X=1)=P(X=2), its mean and variance are
View SolutionLet X be a random variable such that P(X=−2)=P(X−1)=P(X=2)=P(X=1)=16 and P(X=0)=13. Find the mean and variance of X.
View SolutionThe variance of the random variable X having the following distribution is X=x:−2−1012P(X=x):1616131616
View SolutionThe mean and variance of a random variable X having a binomial distribution are 4and2 respectively. The P(X=1) is
View SolutionIn binomial distribution of random variable X if mean = np and variances = npq then
P(X=k)P(X=k−1)=……
View Solution