State Gauss 'law in electrostatics.
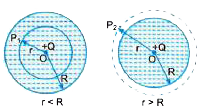
Consider an overall neutral sphere of radius R. This sphere has a point charge +Q at its centre and this positive charge is surrounded by a uniform density ρ of negative charges up to a radius R.
Use Gauss, law to obtain expression for the electric field , of this sphere , at a point distant r, from its centre ,where
r<R,
r>R
Show that these two expressions give identical results, for the electric field, at r= R.
Consider a sphere of radius R and having point charge +Q at its centre point. Negative charges density of sphere be ρ. then total negative charge on sphere =43πR3ρ=−Q
⇒ ρ=−3Q4πR3
For a point P1 situated at a distance r (where r <R) frm its centre, considering a sphere of radius .r. as the Gaussian surface , we have
⇒ ϕ∈=∫→E.→ds=E.4πr21∈0(charged enclosed)
1∈0[Q+ρ.43πr3]
⇒ E.4πr2=1∈0[Q−3Q4πR3.43πr3]=1∈0[Q−Qr3R3]=Q∈0[1−r3R3]
⇒ E=Q4π∈0[1r2−rR3]
For r= R, we have Esurface=0.
(b) For a point P2 situated at a distance r (where r>R) we again consider a spere of radius r as the Gaussian surface. Now total charges enclosed in the surface.
=Q+ρ.43πR3=Q−3Q4πR3.43πR3=Q−Q=0
This shown that ϕ∈=E.4πr2=1∈0 (charge enclosed) =1∈0(0)=0
⇒ E=0
and field at surface of sphere Esurface=0 .
Topper's Solved these Questions
- BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SELF ASSESSMENT TEST (SECTION-A)5videos
ELECTRIC CHARGES AND FIELDS
- BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SELF ASSESSMENT TEST (SECTION-A) (FILL IN THE BLANKS)3videos
ELECTRIC CHARGES AND FIELDS
- BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - LONG ANSWER QUESTIONS -I30videos
ELECTRIC CHARGES AND FIELDS
- BOOK - U-LIKE SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - SELF ASSESSMENT TEST SECTION-C (VERY SHORT ANSWER QUESTIONS)3videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SELF ASSESSMENT TEST (SECTION C)1videos
ELECTROMAGNETIC WAVES
Similar Questions
An early model for an atom considered it to have a positivelly charged point nucleus of charge +Ze surrounded by a uniform density of negative charge up to a radius R. The atom as whole is neutral. For this model , what is the electric field at a distance r from the nucleus when
r<R
r=R ?Use Gauss's theoremView SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View Solution
Knowledge Check
- Question 1 - Select One
A non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
AIncreases as r increases inside the sphereBDecreases as r increases inside as well as outsideCIncreases as increases outside the sphereDIs discontinuousat r=R - Question 2 - Select One
A hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
Adecreases as r increases for r<R and r>RBincreases as r increases for r<R and r>RCzero as r increases for r<R, decreases as r increases for r>RDzero as r increases for r<R, increases for r>R - Question 3 - Select One
A sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
AE=σR2∈0kr2BE=σ∈0kCE=R2DE=∈0kr2σ2
The centre of neutral conducting sphere of radius "R" is at distance 'd' from a point charge "Q" .The potential of the sphere is
View SolutionUsing Gauss. theorem, obtain an expression for intensity of electric field .E. at a point which is at a distance r (r>R) from the centre Cof a thin spherical shell (of radius R) carrying charge.Q.
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be
 View Solution
View SolutionAn insulated sphere of radius r haas a uniform volume charge density λ. The electric field at a point A, which is at distance r from its centre is given by (R>r)
View SolutionIf charge q is induced on outer surface of sphere of radius R, then intensity at a point P at a distance S from its centre is
View Solution
