Consider that an ideal gas (n moles) is expanding in a process given by p = f (V), which passes through a point . Show that the gas is absorbing heat at if the slope of the curve p =f (V) is larger than the slope of the adiabatic passing through . Solution in Gujrati
Slope of graph P=f(V) at point
For adiabatic process =K (Constant)
At point
Slope =....(1)
Now dQ=dU+dW
...(2)
and PV =nRT
...(3)
Equ. (2)
...(4)
Now,
...(5)
Putting value of (5) in (4),
When gas expended then and heat is absorbed.
Now hence ,
Topper's Solved these Questions
- THERMODYANMICS Book:KUMAR PRAKASHANChapter:THERMODYANMICS Exercise:Section-E MCQs
Explore 42 Videos
- THERMODYANMICS Book:KUMAR PRAKASHANChapter:THERMODYANMICS Exercise:Section-F Questions from Module
Explore 20 Videos
- THERMODYANMICS Book:KUMAR PRAKASHANChapter:THERMODYANMICS Exercise:Section-D Ncert Exemplar Solution (Short Answer )
Explore 6 Videos
- THERMAL PROPERTIES OF MATTERBook:KUMAR PRAKASHANChapter:THERMAL PROPERTIES OF MATTERExercise:Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks
Explore 1 Video
- UNITS AND MEASUREMENTBook:KUMAR PRAKASHANChapter:UNITS AND MEASUREMENTExercise:Section -F (Questions from Module )
Explore 20 Videos
Similar Questions
Heat absorbed by the gas undergo a cylic process along closed path in one complete cycle as shown in figure will be _____ J.
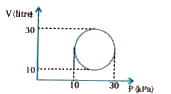
View SolutionIn a thermodynamics process which one of the following statement is not true ?
View SolutionConsider a Carnot's cycle operating between T1 = 500 K and T2 = 300 K producing 1 kJ of mechanical work per cycle. Find the heat transferred to the engine by the reservoirs.
View SolutionIn an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150∘C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27∘C. The final temperature is 40∘C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal ?
View SolutionIf the error in measurement of radius of a shpere is 2% then the error in determination of volume of the sphere will be …………
View Solutionn moles of a monoatomic gas are taken around in a cyclic process consisting of four processes along ABCDA as shown. All the lines on the p-V diagram have slope of magnitude p0/V0. The pressure at A and C is p0andthevolumesatAandCareV_0//2and3V_0//2, respectively. Calculate the percentage efficiency of the cycle.

View SolutionThe internal energy of a gas is given by U=2pV . It expands from V_0 to 2V_0 against a constant pressure p_0 . The heat absorbed by the gas in the process is
View SolutionConsider that an ideal gas (n mol es) is expanding in a process given by P=f(V) , which passes through a point (P_(0), V_(0)) . Show that the gas is absorbing heat at (P_(0), V_(0)) if the slope of the curve P=f(V) is larger than the slope of the adiabat passing through (p_(0), V_(0)) .
View SolutionAn ideal gas with the adiabatic exponent gamma goes through a process p = p_0 - alpha V , where p_0 and alpha are positive constants, and V is the volume. At what volume will the gas entropy have the maximum value ?
View SolutionOne mole of an ideal gas passes through a process where pressure and volume obey the relation P=P_0 [1-1/2 (V_0/V)^2] Here P_0 and V_0 are constants. Calculate the change in the temperature of the gas if its volume changes from V_0 to 2V_0 .
View SolutionOne mole of diatomic gas undergoes a process P=(P_0)/([1+(V//V_0)^3]) , where P_0 and V_0 are constants . The translational kinetic energy of the gas when V=V_0 is given by
View SolutionOne mole of the ideal gas through the process p=p0[1−α(VV0)3] , where p and V are pressure and volume p0,V0 and α are constant . If the maximum attainable temperature of the gas is (34)p0V0R , then the value of α is
View Solution1 mol of an ideal gas obeys the following equations p=p_0/(1+(V_0//V)^2) where p_0 and V_0 are constants. Find the change in temperature the volume of the gas is doubled.
View SolutionConsider that an ideal gas (n Moles) is expanding in a process given by P=f (V), which passes through a ponts (V0,P0) . Show that the gas is absorbing heat at (P0,V0) if the slope of the curve P=f(v) is larger that the slope of the adiabat passing through (P0,V0) .
View SolutionConsider that an ideal gas (n moles) is expanding in a process given by P=f(V), which passes through a point (V0,P0). Show that the gas is absorbing heat at (P0,V0) if the slope of the curve P=f(V) is larger than the slope of the adiabat passing through (P0,V0).
View Solution