Show four steps of carnot engine in P-V graph write the equation of each step and obtain the work done by the system. Also obtain the efficiency of a carnot engine.Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

There are four reversible process occur in carnot engine.
(1) isothermal expansion
(2) Adiabatic expansion
(3) Isothermal compression
(4) Adiabatic compression
A cylic process is obtain by these four processes is shown in below P $\to$ V diagram.

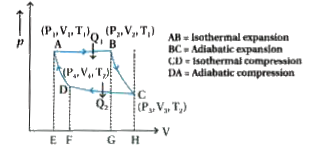
(a) Step 1: Isothermal expansion of gas taking its state from $(P_{1}, V_{1}, T_{1})$ to $(P_{2}, V_{2}, T_{1})$ . For this, the conducting bottom of the cylinder is brought into contact with the heat and the gas is slowly allowed to expand isothermally.
(b) The heat absorbed by the gas $Q_{1}$ from the reservoir, hence work done by gas (or on surrounding)
$W_{1} = Q_{1} = μ R T_{1} ln (\frac{V_{2}}{V_{1}})$ ...(1)
Where $μ$ is amount of gas in mole
R=Gas constant or $W_{1} = Q_{1}$ =Area of ABGEA
(b) Step 2: (Adiabatic expansion) : Now, the cylinder is placed on a thermally insulated stand and gas is adiabatically expanded from state $(P_{2}, V_{2}, T_{1})$ to $(P_{3}, V_{3}, T_{2})$ (Here temperature decreases due to expansion). The work done by the gas in adiabatic expansion (or on surrounding)
$W_{2} = \frac{μ R (T_{1} - T_{2})}{γ - 1}$ ...(2)
OR
$∴ W_{2}$ = Area of BCHGB
(c) Step 3: (Isothermal compression): Now the cylinder is brought in contact with heat sink and isothermally compressed slowly and brought from $(P_{3}, V_{3}, T_{2})$ to $(P_{4}, V_{4}, T_{2})$ . During this process heat released $Q_{2}$ by the gas to the reservoir (sink) at temperature $T_{2}$ . The work done on the gas (or by surrounding)
$W_{3} = - Q_{2} = - μ R T_{2} ln (\frac{V_{4}}{V_{3}})$
$∴ W_{3} = Q_{2} = μ R T_{2} ln (\frac{V_{3}}{V_{4}})$ ...(3)
(Here work done on the system and system rejected heat so W and $Q_{2}$ are negative)
OR $W_{3} = Q_{2}$ =Area of CDFHC
(d) Step 4: (Adiabatic compression): Now the cylinder is placed on a thermally insulated stand and the gas is compressed adiabatically and is taken from state to $[P_{4}, V_{4}, T_{2}]$ to $[P_{1}, V_{1}, T_{1}]$
The work done on the gas (work done by surrounding) in adiabatic compression.
$W_{4} = - \frac{μ R [T_{2} - T_{1}]}{γ - 1}$
$∴ W_{4} = \frac{μ R [T_{1} - T_{2}]}{γ - 1}$ ....(4)
OR $W_{4}$ = Area of ADFEA
Total work done by the gas in one complete cycle from equation (1),(2),(3) and (4) ,
$W = W_{1} + W_{2} \to (- W_{3}) + (- W_{4})$
But $W_{2} = W_{4}$
[ $∵ W_{2}$ is the work done by gas and $W_{4}$ is the work done on the gas]
$∴ W = W_{1} - W_{3}$ ...(5)
$[∵ W_{1} > 0, W_{3} < 0]$
=Area of ABCDA
Now efficiency of engine,
$η = \frac{W}{Q_{1}}$
$= \frac{W_{1} - W_{3}}{Q_{1}} = \frac{Q_{1} - Q_{2}}{Q_{1}}$
$= 1 - \frac{Q_{2}}{Q_{1}}$
$∴ η = 1 - \frac{μ R T_{2} ln (\frac{V_{3}}{V_{4}})}{μ R T_{1} ln (\frac{V_{2}}{V_{1}})}$
$∴ η = 1 - \frac{T_{2} ln (\frac{V_{3}}{V_{4}})}{T_{1} ln (\frac{V_{2}}{V_{1}})}$ ...(6)
(From equ. (1) and (3))
For adiabatic process $T V^{γ - 1}$ = constant
$∴$ For step $\to$ 2
$T_{1} V_{2}^{γ - 1} = T_{2} V_{3}^{γ - 1}$
$∴ {(\frac{V_{2}}{V_{3}})}^{γ - 1} = \frac{T_{2}}{T_{1}}$
$∴ \frac{V_{2}}{V_{3}} = {(\frac{T_{2}}{T_{1}})}^{\frac{1}{γ - 1}}$ ...(7)
and for step $\to$ 4
$\frac{V_{1}}{V_{4}} = {(\frac{T_{2}}{T_{1}})}^{\frac{1}{γ - 1}}$ ....(8)
From equation (7) and (8) ,
$\frac{V_{2}}{V_{3}} = \frac{V_{1}}{V_{4}}$
$∴ \frac{V_{2}}{V_{1}} = \frac{V_{3}}{V_{4}}$ ....(9)
From equation (6) and (9) ,
$η = 1 - \frac{T_{2}}{T_{1}}$ is the efficiency of carnot engine

Updated on:21/07/2023

|

Class 11 PHYSICS THERMODYANMICS

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-THERMODYANMICS -Question Paper

Home
Ask Doubt
Profile