Line L is tangent to unit circle S at point P .Point A and the circle S are on the same side of L and the distance from A to L is 3 units.Two tangents from point A intersect line L at point B and C then the value of PB.PC is equal to
Step by step video & image solution for Line L is tangent to unit circle S at point P .Point A and the circle S are on the same side of L and the distance from A to L is 3 units.Two tangents from point A intersect line L at point B and C then the value of PB.PC is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Length of tangent from an external point p to the circle S=0 is
View SolutionPA and PB are tangents to a circle S touching it at points A and B. C is a point on S in between A and B as shown in the figure. LCM is a tangent to S intersecting PA and PB in S at points L and M, respectively. Then the perimeter of the triangle PLM depends on o
View Solution
Knowledge Check
Distance of a point P on the parabola y2=48x from the focus is l and its distance from the tangent at the vertex is d then l-d is equal to
A4B8C12D16PA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
A43∘B53∘C50∘D20∘
The point C is the image of point A in line l and line segment BC intersects the line l at P.
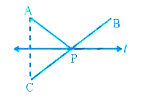
Is PA = PC ?
View SolutionTANGENT : Intersection point of line and Circle are Coincident.
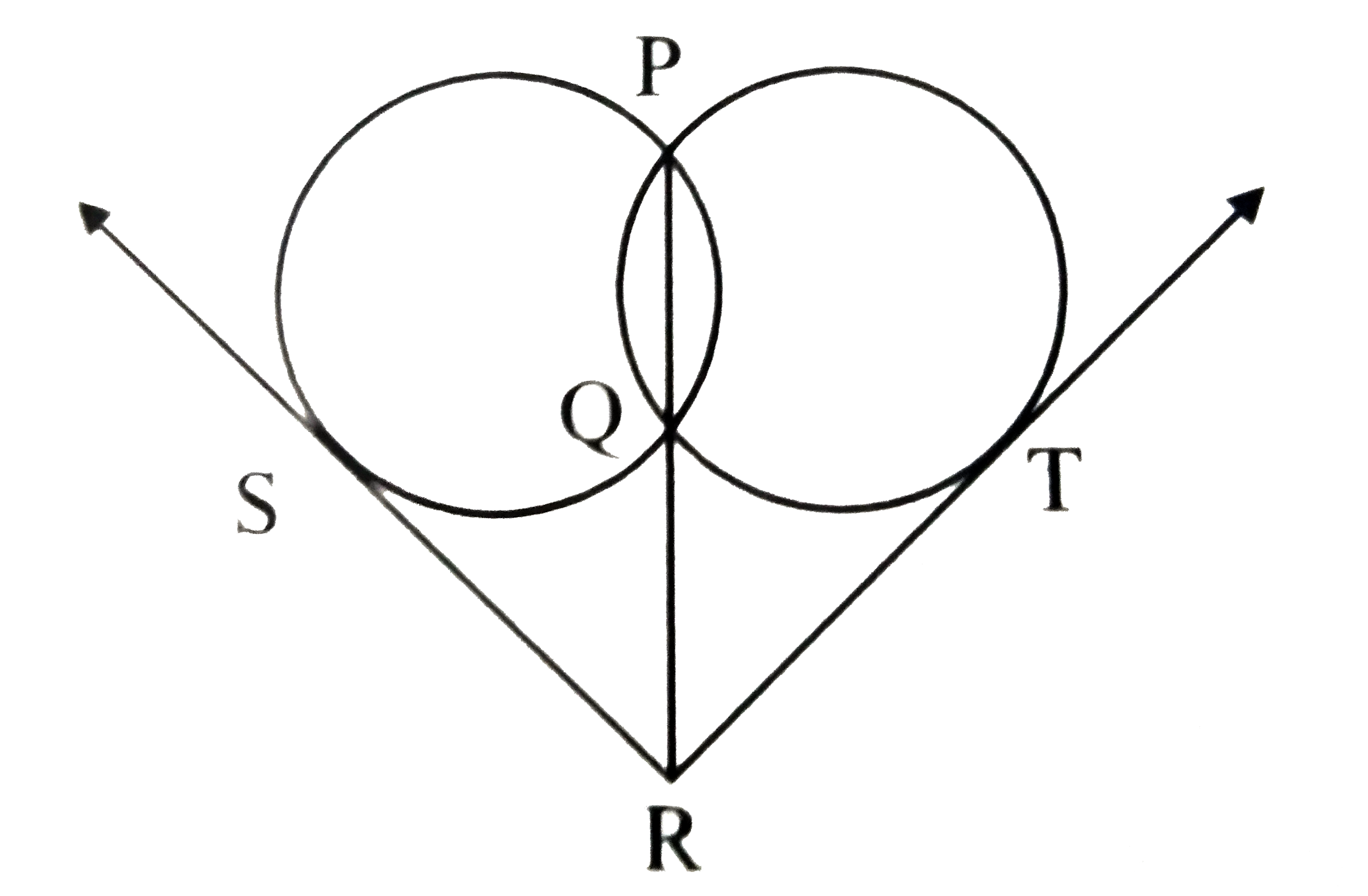
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.
View SolutionTwo tangents are drawn from a point P on the circle at point A and B. O is the centre of the circle. If ∠AOP=60∘ then find ∠APB.
View SolutionThe equation of any circle passing through the points of intersection of the circle S=0 and the line L=0 is
View SolutionPA and PB are the two tangents drawn on a circle from and external point P. The centre of the circle is O and the tangents touches the circles at points A and B. Then quadrilateral OAPB is-
View Solution
