यदि log1/2(4−x)≥log1/22−log1/2(x−1) है, तब x के मानो का समुच्चय है
(1,2]
[3,4)
(1,3]
[1,4)
The correct Answer is:A, B
Step by step video, text & image solution for यदि log_(1//2) (4-x) ge log_(1//2) 2-log_(1//2) (x-1) है, तब x के मानो का समुच्चय है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - लघुगणक और आंशिक भिन्नें EXERCISE - JEE Advanced (integer type questions)8videos
लघुगणक और आंशिक भिन्नें
- BOOK - ERRORLESS HINDICHAPTER - लघुगणक और आंशिक भिन्नें EXERCISE - Exercise36videos
लघुगणक और आंशिक भिन्नें
- BOOK - ERRORLESS HINDICHAPTER - फलन, सीमा, सांतत्य तथा अवकलनीयताEXERCISE - JEE ADVANCED( MATCH THE COLUMN TYPE)13videos
फलन, सीमा, सांतत्य तथा अवकलनीयता
- BOOK - ERRORLESS HINDICHAPTER - वर्ग समीकरण एवं असमिकायें EXERCISE - JEE Advanced (Matrix Match type questions)2videos
वर्ग समीकरण एवं असमिकायें
Similar Questions
पद 6+log32⎛⎜ ⎜⎝13√2 ⎷4−13√2 ⎷4−13√2√4−13√2…⎞⎟ ⎟⎠ का मान है
08:52View Solutionयदि a,b,c भिन्न धनात्मक संख्याये है एवं 1 से भिन्न इस प्रकार है, कि [logbalogca−logaa]+[logablogcb−logbb]+[logaclogbc−logcc]=0 तो abc=
03:16View Solutionकॉलम I में दिए गए वक्तव्यों/व्यंजकों का कॉलम II में दिये गये मानों से सुमेल करे।
03:32View Solution
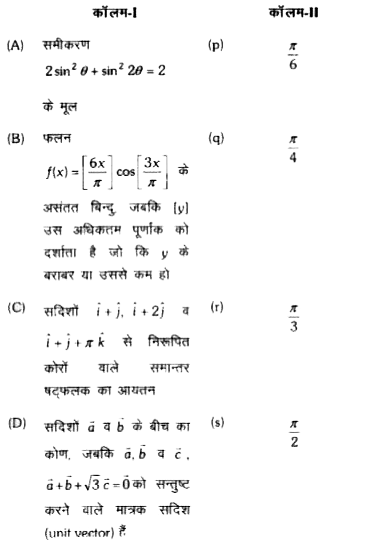
04:39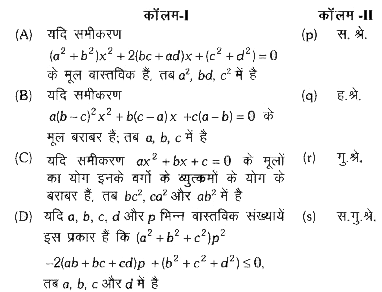View Solutionlog_((3)/(4))log_(8)(x^(2)+7)+log_((1)/(2))log_((1)/(4))(x^(2)+7)^(-1)=-2
07:03View Solutionlog_(2)(x^(2)-1)=log_((1)/(2))(x-1)
08:44View Solution(1)/(log_(2)x)+(1)/(log_(3)x)+......(1)/(log_(43)x)=(1)/(log_(43)!x)
02:16View Solutionlog_(2)(4^(x)+4)=log_(2)2^(x)+log_(2)(2^(x+1)-3)
02:48View Solutionlog_(4)(x^(2)-1)-log_(4)(x-1)^(2)=log_(4)sqrt((4-x)^(2))
02:06View Solutionlog_((3)/(4))log_(8)(x^(2)+7)+log_((1)/(2))log_((1)/(4))(x^(2)+7)^(-1)=-2
09:07View Solutionlog_(2)sin x-log_(2)cos x-log_(2)(1-tan x)-log_(2)(1+tan x)=-1
03:49View SolutionIf log1/2(4−x)≥log1/22−log1/2(x−1),then x belongs to
03:39View SolutionIf log1/2(4−x)≥log1/22−log1/2(x−1), then x can belong to
04:15View Solutionयदि log2(5⋅2x+1),log4(21−x+1) और 1 समान्तर श्रेणी में है, तब x=
02:54View Solutionlog4(x−1)=log2(x−3) के हलों की संख्या है
07:08View Solution