Derive formula for mutual inductance for two very long coaxial solenoids. Also discuss reciprocity theorem.Solution in Gujrati
Consider figure which shows two long coaxial solenoids each of length l. We denote the radius of the inner solenoid S1 by r1 and the number of turns per unit length by n1. The corresponding quantities for the outer solenoid S2 are r2 and n2 respectively. Let N1 and N2 be the total number of turns of coils S1 and S2 respectively.
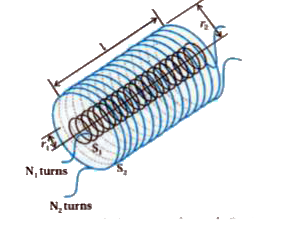
When a current I2 is set up through S2, it in turn sets up a magnetic flux through S1. Let us denote it by Φ1.
The corresponding flux linkage with solenoid S1 is
∴N1Φ1=M12I2 ....(1)
M12 is called the mutual inductance of solenoid S1 with respect to solenoid S2. It is also referred to as the coefficient of mutual induction.
N1Φ1=N1A1B2
N1Φ1=(n1l)(πr21)(μ0n2I2)
=μ0n1n2πr21π2...(2)
Where n1l is the total number of thuns in solenoid S1 . Thus, from equation (1) and (2) , M12=μ0n1n2πr21l...(3)
Note that we neglected the edge effects and considered the magnetic field μ0n2I2 to be uniform throughout the length and width of the solenoid S2.
We now consider the reverse case. Current I1 is passed through the solenoid S1 and the flux linkage with coil S2 is,
N2Φ2=M21I1..(4)
M21 is called the mutual inductance of solenoid S2 with respect to solenoid S1.
The flux due to the current I1 in S1 can be assumed to be confined solely inside S1 since the solenoids are very long. Thus, flux linkage with solenoid S2 is
N2Φ2=N2A1B1
N2Φ2=(n2I)(πr21)(μ0n1I1)
=μ0n1n2πr21π1....(5)
Where n2I is the total number of turns of S2. From equation (4) to (5),
M21=μ0n1n2πr21l...(6)
Using equation (3) and (6), we get
M12=M21=M (say)...(7)
Equation (7) is known as reciprocity theorem.
We have considered air as a medium in solenoid. Instead of air medium of relative permeability μ is considered then
M=μn1n2πr2l
μ=μ0μr=(μ0μr)n1n2πr2l
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section A (Try yourself )
36 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section A HOTS
2 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION D MCQS ASKED IN COMPETITIVE EXAMES (MCQS AKSED IN BOARD EXAM AND GUJCET)
14 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
5 Videos
Similar Questions
Which scientist established that electricity and magnetism are interrelated ?
View SolutionGive the explanation of reason behind the origin of motional induced emf.
View SolutionWhen air is replaced by dielectric medium of constant K, the maximum force of attraction between two charges separated by distance d, ..........
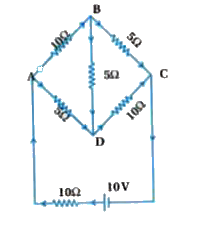
View SolutionDetermine the current in each branch of the given network.
View SolutionObtain an expression for the mutual inductance of two long co-axial solenoids.
View Solutionदो लम्बी समअक्षीय परिनालिकाओं के मध्य अन्योन्य प्रेरकत्व के लिए व्यंजक स्थापित कीजिए तथा बताइये की यह किन-किन कारकों पर निर्भर करता है?
View Solutionअन्योन्य प्रेरकत्व गुणांक किसे कहते हैं, यह सदिश राशि है या अदिश किसी दो लौह समाक्षीय परिनालिका का अन्योन्य प्रेरकत्व 3.0H है। क्रोड को हटाने पर अन्योन्य प्रेरकत्व 1.5H हो जाता हैं। उपयोग किए गए क्रोड की आपेक्षिक चुंबकनशीलता क्या हैं?
View SolutionExplain the mutual induction between two long solenoids. Obtain an expression for the mutual inductance.
View Solutionअन्योन्य प्रेरकत्व पद को परिभाषित कीजिए। दो लंबी समाक्षीय परिनालिकाओं, जिनकी त्रिज्याएँ और फेरों की संख्याएँ भिन्नभिन्न हैं, के अन्योन्य प्रेरकत्व हेतु व्यंजक व्युत्पन्न कीजिए।
View Solutionअन्योन्य प्रेरण क्या है ? व्याख्या कीजिये | अन्योन्य प्रेरकत्व की परिभाषा एवं SI मात्रक लिखिए | दो लम्बी समाक्ष परिनालिकाओं के अन्योन्य प्रेरकत्व के लिए सूत्र निगमित कीजिये |
View SolutionCalculate the self-inductance for very long solenoid.
View SolutionDefine mutual inductance between a pair of coils. Derive expression for the mutual inductance of two long coaxial solenoids of same length wound one over the other.
View SolutionDerive an expression for the coefficient of self-induction of a long solenoid.
View SolutionDefine the term .mutual inductance. between the two coils. Obtain the expression for mutual inductance of a pair of long coaxial solenoids each of length l and radii r1 and r2(r2>>r1). Total number of turns in the two solenoids are N1 and N2 respectively.
View SolutionDerive expression for the coefficient of mutual inductance between two long solenoids.
View Solution
