घूर्णन गति की तीन समीकरणω=ω0+αt,θ=ω0t+12αt2 तथा ω2−ω20=2αθ हैं, जहाँ संकेतक अपने प्रायोगिक मान में हैं। यद्यपि v=rω,ω=2πT=2πn मानक सम्बन्ध हैं। इनका उपयोग करते हुए निम्न प्रश्नों के उत्तर दो
एक वाशिंग मशीन जिसके चक्रण का घूर्णन 15 चक्र/से से घटकर 5 चक्र/से हो जाता है जबकि यह 50 घूर्णन करता है। चक्रण का कोणीय त्वरण है
−4π रेडियन//से2
4π रेडियन//से2
8π रेडियन//से2
−8π रेडियन//से2
The correct Answer is:B
n0=15 चक्र/से, n=5 चक्र/से
θ=50 घूर्णन =50×2 रेडियन
ω2−ω20=2αθ से
α=ω2−ω202θ=4π2(n2−n20)2θ
α=4π2(52−152)2×5×2π=−4π रेडियन//से2
Topper's Solved these Questions
- घूर्णन गति Book:ARIHANT HINDIChapter:घूर्णन गति Exercise:प्रश्नावली स्तर 2 (दृढ़कथन-कारण प्रकार निर्देश)
Explore 5 Videos
- घूर्णन गति Book:ARIHANT HINDIChapter:घूर्णन गति Exercise:प्रश्नावली स्तर 2 विगत वर्षो के प्रश्न
Explore 23 Videos
- घूर्णन गति Book:ARIHANT HINDIChapter:घूर्णन गति Exercise:प्रश्नावली स्तर 2 प्रश्नावली एक या एक से अधिक विकल्प सही हैं
Explore 6 Videos
- घूर्णन Book:ARIHANT HINDIChapter:घूर्णन Exercise:प्रश्नावली (विगत वर्षो के प्रश्न)
Explore 22 Videos
- ठोस एवं अर्ध्दचालक युक्तियाँ Book:ARIHANT HINDIChapter:ठोस एवं अर्ध्दचालक युक्तियाँ Exercise:प्रश्नावली स्तर 2 विगत वर्षों के प्रशन
Explore 9 Videos
Similar Questions
वक्तव्य I किसी पिण्ड का द्रव्यमान केन्द्र उसके आकार के बदलने पर बदल जाता है।
वक्तव्य II r=∑i=ni=1miri∑i=ni=1mi
View Solutionस्पर्शरेखीय लगाये गये बल F=(20t−5t2) न्यूटन (जहाँ t सेकण्ड में नापा गया है) के कारण 2 मी त्रिज्या की एक घिरनी अपनी अक्ष पर घूर्णन करती है। यदि घूर्णन अक्ष के इर्द-गिर्द, घिरनी का जड़त्व आघूर्ण 10 किग्रा-मी2 है, तब घिरनी की गति की दिशा प्रतिलोमित होने से पहले घिरनी द्वारा किये गये चक्करों की संख्या है
View Solutionसाइकिल का एक पहिया एक खुरदी सड़क पर बिना फिसले एक रेखीय चाल से चित्रानुसार चलता है, तब
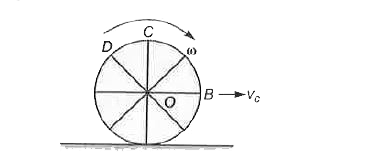
View Solutionएक द्विपरमाणुक अणु m1 तथा m2 के दो द्रव्यमानो से बना है जोको दूरी r पर है यदि कोणीय संवेग क्वाण्टीकरण के बोर के नियम को लगाकार हम इसकी घूर्णन ऊर्जा की गणना करें तब इसकी ऊर्जा दी जाएगी (n एक पूर्णांक है)
View SolutionOR गेट के निर्गत को NAND गेट के दोनों निवेशों से जोड़ा जाता है। संयोजन इस भाँति कार्य करेगा
View SolutionThe differential equation satisfied by y=A sin(omega t+omega_(0))+B cos(omega t+omega_(0))(omega,omega_(0) are known constant) is
View Solutionसिद्ध कीजिए -
(i) ω=ω0+αt,
View Solutionसिद्ध कीजिए -
(ii) θ=ω0t+12αt2
View Solutionयदि समीकरण (a2+4a+3)x2+(a2−a−2)x+a(a+1)=0 के दो से अधिक मूल हैं, तो a का मान है
View Solutionयदि समीकरण x2+x+1=0 के मूल a,b हैं तथा x2+px+q=0 के मूल हैं, ab,ba तो p+q का मान है
View Solutionनिम्न में से कौन-सा कथन सत्य हैं ?
"sec A का मान-1 और 1 के बीच में होता है
View Solutionघूर्णन गति की तीन समीकरणे ω=ω0+αt,θ=ω0t+12αt2 तथा ω2−ω20=2αθ हैं, जहाँ संकेतक अपने प्रायोगिक मान में हैं। यद्यपि v=rω,ω=2πT=2πn मानक सम्बन्ध हैं। इनका उपयोग करते हुए निम्न प्रश्नों के उत्तर दो
घड़ी की मिनट वाली सुईं की कोणीय चाल है
View Solutionघूर्णन गति की तीन समीकरणे ω=ω0+αt,θ=ω0t+12αt2 तथा ω2−ω20=2αθ हैं, जहाँ संकेतक अपने प्रायोगिक मान में हैं। यद्यपि v−rω,ω=2πT=2πn मानक सम्बन्ध हैं। इनका उपयोग करते हुए निम्न प्रश्नों के उत्तर दो
5 सेमी नोक वाली घण्टे की सुईं का रेखीय वेग है
View Solutionघूर्णन गति की तीन समीकरणे ω=ω0+αt,θ=ω0t+12αt2 तथा ω2−ω20=2αθ हैं, जहाँ संकेतक अपने प्रायोगिक मान में हैं। यद्यपि v−rω,ω=2πT=2πn मानक सम्बन्ध हैं। इनका उपयोग करते हुए निम्न प्रश्नों के उत्तर दो
एक 20 किग्रा का ठोस बेलन अपने अक्ष पर 100 रेडियन/से के कोणीय संवेग से घूम रहा है। बेलन की त्रिज्या 0.25 मी है। बेलन के घूर्णन की गतिज ऊर्जा क्या है? बेलन का उसके अक्षों के सापेक्ष कोणीय संवेग का परिमाण क्या है?
View Solutionघूर्णन गति की तीन समीकरणे ω=ω0+αt,θ=ω0t+12αt2 तथा ω2−ω20=2αθ हैं, जहाँ संकेतक अपने प्रायोगिक मान में हैं। यद्यपि v−rω,ω=2πT=2πn मानक सम्बन्ध हैं। इनका उपयोग करते हुए निम्न प्रश्नों के उत्तर दो
समान परिमाण का बलाघूर्ण एक खाली बेलन तथा ठोस गोले पर लगाया जाता है। दोनों के द्रव्यमान तथा त्रिज्या समान है। बेलन अपने मानक अक्षों के परितः घूमने के लिए पूर्णतः स्वतन्त्र है, तथा गोला अपने केन्द्र से जाने वाले अक्षों के परितः घूमने के लिए पूर्णतः स्वतन्त्र है। निश्चित समय के बाद दोनों में किसकी कोणीय चाल अधिक होगी?
View Solution

