Is a two-digit integer 'x' dividible by 12?
I. When 'x' is divided by 5, the remainder is 2.
II. When 'x' is divided by 3, the remainder is 1.
if the data in statement I alone are sufficient to answer the questin, while the data in statement II alone are not sufficient to answer the question.
if the data in statement II alon are sufficient to answer the question, while the data in statement I alone are not sufficient to answer the question.
if the data either in statement I alone or in statement II alone in sufficient to answer the question.
if the data even in both the statements I and II together are not sufficient to answer the question.
The correct Answer is:B
To determine whether a two-digit integer x is divisible by 12, we need to analyze the two statements provided.
Step 1: Understand the divisibility rule for 12
A number is divisible by 12 if it is divisible by both 3 and 4. Therefore, we need to check if x meets these criteria.
Step 2: Analyze Statement I
Statement I: When x is divided by 5, the remainder is 2.
This means:
x=5k+2
for some integer k.
However, this statement does not provide any information about the divisibility of x by 3 or 4. Therefore, we cannot conclude whether x is divisible by 12 based solely on this statement.
Conclusion from Statement I: Not sufficient.
Step 3: Analyze Statement II
Statement II: When x is divided by 3, the remainder is 1.
This means:
x=3m+1
for some integer m.
Since x leaves a remainder of 1 when divided by 3, it cannot be divisible by 3. Consequently, if x is not divisible by 3, it cannot be divisible by 12 (since 12 requires divisibility by both 3 and 4).
Conclusion from Statement II: Sufficient to conclude that x is not divisible by 12.
Final Conclusion
- Statement I alone is not sufficient.
- Statement II alone is sufficient.
Thus, the answer is that only Statement II is sufficient to determine whether x is divisible by 12.
---
A number is divisible by 12 if it is divisible by both 3 and 4. Therefore, we need to check if x meets these criteria.
Statement I: When x is divided by 5, the remainder is 2.
x=5k+2
for some integer k.
Statement II: When x is divided by 3, the remainder is 1.
x=3m+1
for some integer m.
- Statement I alone is not sufficient.
- Statement II alone is sufficient.
Topper's Solved these Questions
Similar Questions
There are two positive integers X & Y. When X is divided by 237, the remainder is 192. When Y is divided by 117 the quotient is the same but the remainder is 108. Find the remainder when the sum of X & Y is divided by 118.
View SolutionLet there are two positive integers a and b where a > b. Now when a is divided by b remainder is 24 and when 2a is divided by b remainder is 11. Find b.
View Solution
Knowledge Check
When 121012 is divided by 12, the remainder is
A0B2C3D4When 121012 is divided by 12, the remainder is
A0B2C3D4When 121012 is divided by 12, the remainder is
A0B2C3D4
When
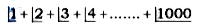 is divided by 12, the remainder obtained is?
is divided by 12, the remainder obtained is?
View SolutionWhen
 is divided by 12 then the remainder will be?
is divided by 12 then the remainder will be?
View SolutionWhen
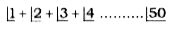 , is divided by 12, the remainder obtained is ?
, is divided by 12, the remainder obtained is ?
View SolutionThe remainder when x45 is divided by x2−1 is
View SolutionFind the remainder when x5 is divided by x2−9.
View Solution