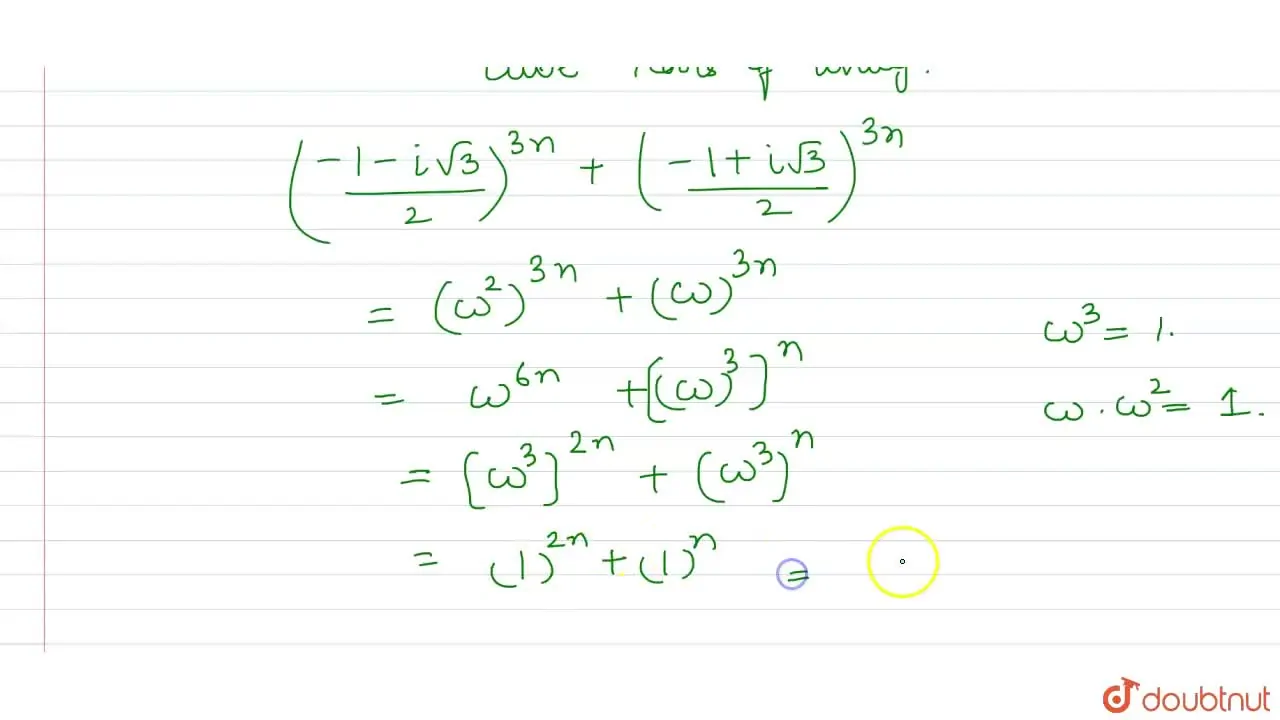What is the value of (1=−+i√32)3n+(−1+i√32)3nwherei=√−1?
A
3
B
2
C
1
D
0
Video Solution
Text Solution
The correct Answer is:B
From cube root of unity
ω=−1+√3i2and
ω2=−1−√3i2
ω3=(−1+√3i2)(−1√3i2)
=(−1)2−(√3i)24=44=1
∴ω3=1
Now, (ω)3n+(ω2)3n
=1+1=2
|
Updated on:21/07/2023
Related Playlists
Similar Questions
What is the value of (−1+i√32)3n+(−1−i√32)3n, where i=√−1?
View SolutionWhat is the value of :
(−1+i√32)3n+(−1−i√32)3n
Where, i=√−1?View Solutionthe value of (−1+√3i2)3n+(−1−√3i2)3n=
View SolutionWhat is the value of (−1+i√3)48?
View SolutionWhat is the value of
[−1+i√3)/2]10+[−1−i√3)/2]10View SolutionFind the values of (1+i√3)3
View SolutionThe value of (−1+i√32)n+(−1−i√32)n where n is not a multiple of 3 and i=√−1 is :
View SolutionFind the argument of −1−i√3
View SolutionWhat is the value of the sum 11∑n=2(in+in+1), where i=√−1 ?
View SolutionThe argument of (1−i√3)(1+i√3) is
View Solution