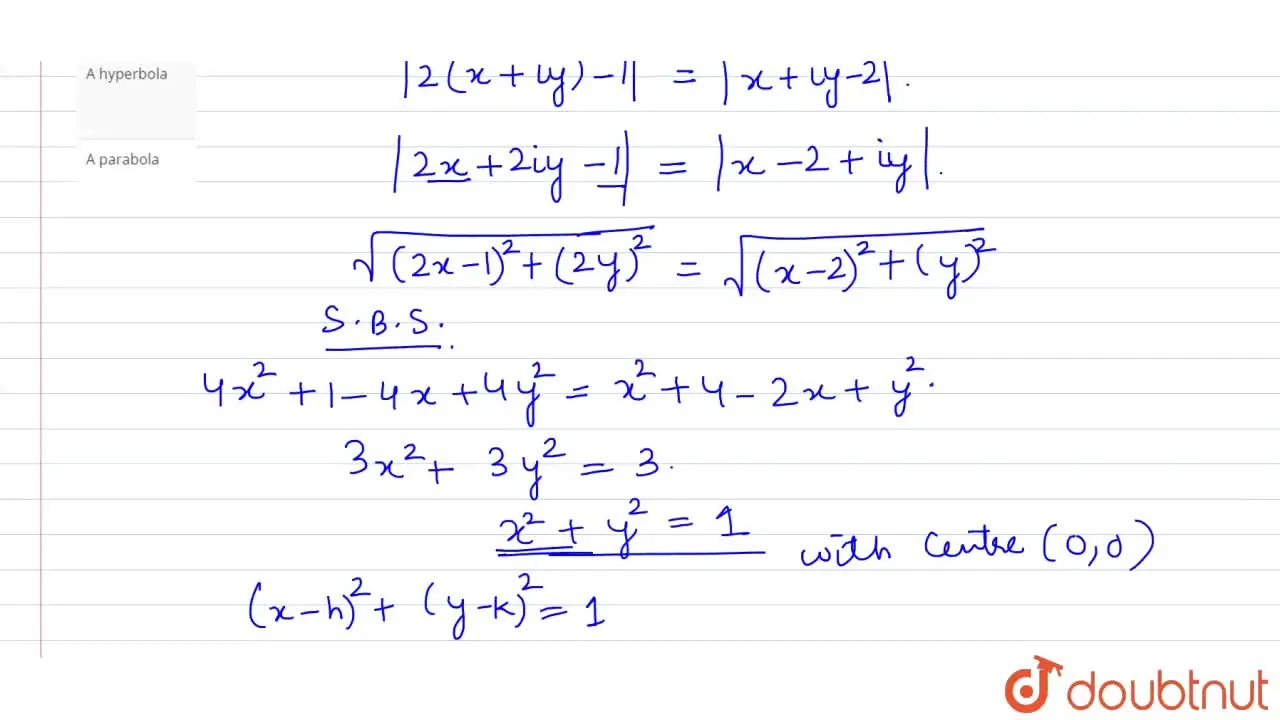Let z=x+iy where x,y are real variable i=√−1. If |2z−1|=|z−2|,then the point z describ es :
A circle
An ellipse
A hyperbola
A parabola
The correct Answer is:A
|2z−1|=|z−2|
|2(x+iy)−1|=|x+iy−2|
|(2x−1)+2yi|=|(x−2)+iy|
√(2x−1)2+y2=√(x−2)2+y2
Squaring both sides
4x2+1−4x+4y2=x2+4−4x+y2
⇒3x2+3y2=3
⇒x2+y2=1
It is the equation of a circle.
∴ The point z describes a circle.
Related Playlists
Similar Questions
Let z=x+iy, where x, y are real variable and i=√−1. If |2z−1|=|z−2|, then the piont z describes
View SolutionSuppose z = x + iy where x and y are real numbers and i=√−1. The points (x, y) for which z−1z−1 is real, lie on
View SolutionLet z=x+iy. If |z–2|=2|z−1|, then |z|2
View SolutionLet z=x+iy, where x,y∈R and i=√−1. Find the radius of circle inscribed in the triangle formed by locus of P(z) satisfying z2−1z2+1∈R and the line 4x+3y=12.
View SolutionLet 2 = x + iy, where x and y are real. The points (x, y) in the X-Yplane or which z+1z−1 purely imaginary lie on
View SolutionLet z=x+iy, where x and y are real. Thepoints (x,y) in the X−Y plane for which z+iz−i is purely imaginary lie on
View SolutionIf z+√2|z+1|+i=0andz=x+iy, then
View SolutionStatement -1 If x,y,z be real variables satisfying x+y+z=6 and xy+yz+z=8, the range of variables x,y and z are identical.
Statement -2 x+y+z=6 and xy+yz+zx=8 remains same if x,y,z interchange their positions.View SolutionIf Re(z−12z+i)=1, where z=x+iy ,then the point (x,y) lies on a
View SolutionIf∣∣∣z+42z−1∣∣∣=1, where z=x+iy. Then the point (x,y) lies on a:
View Solution