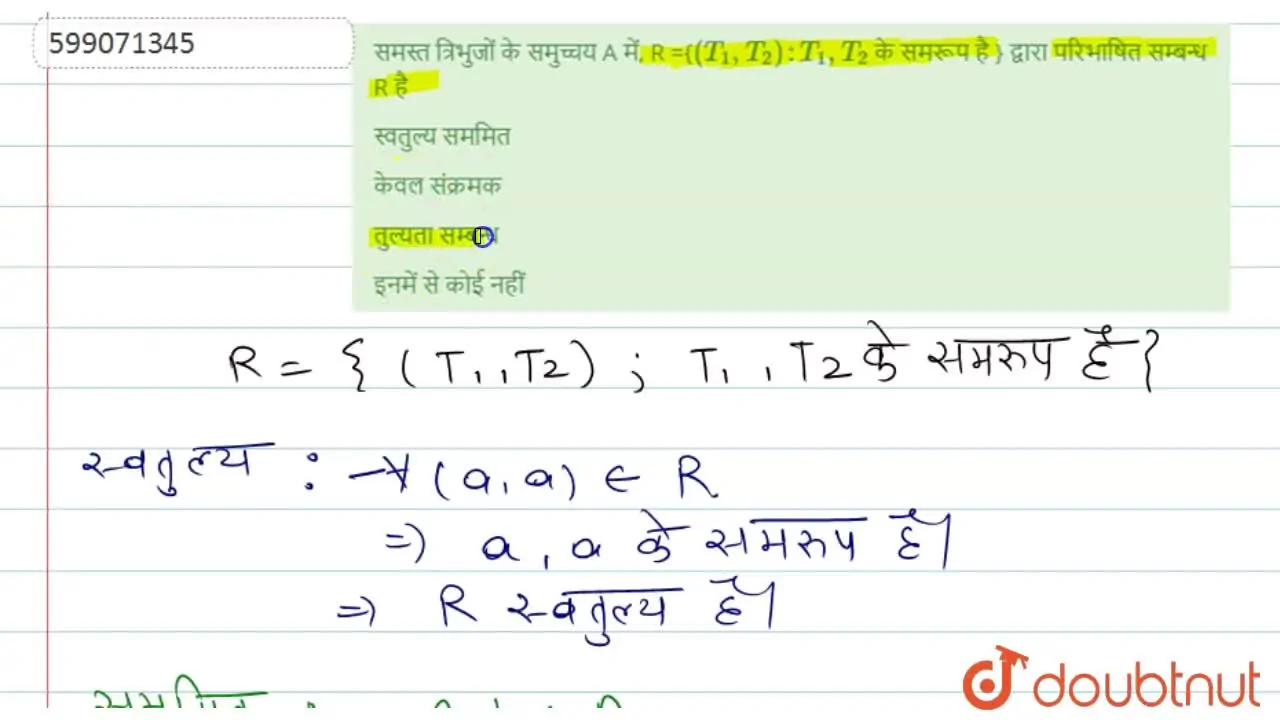
समस्त त्रिभुजों के समुच्चय A में, R ={(T1,T2):T1,T2 के समरूप है } द्वारा परिभाषित सम्बन्ध R है
स्वतुल्य सममित
केवल संक्रमक
तुल्यता सम्बन्ध
इनमें से कोई नहीं
The correct Answer is:C
Step by step video, text & image solution for समस्त त्रिभुजों के समुच्चय A में, R ={(T_1,T_2):T_1,T_2 के समरूप है } द्वारा परिभाषित सम्बन्ध R है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ARIHANT HINDICHAPTER - सम्बन्ध तथा फलन EXERCISE - प्रश्नावली स्तर 2 (केवल एक विकल्प सही है)17videos
सम्बन्ध तथा फलन
- BOOK - ARIHANT HINDICHAPTER - सम्बन्ध तथा फलन EXERCISE - प्रश्नावली स्तर 2 (एक से अधिक विकल्प सही है )2videos
सम्बन्ध तथा फलन
- BOOK - ARIHANT HINDICHAPTER - सम्बन्ध तथा फलन EXERCISE - साधित उदाहरण12videos
सम्बन्ध तथा फलन
- BOOK - ARIHANT HINDICHAPTER - समुच्चय , सम्बन्ध तथा फलन EXERCISE - प्रश्नावली (विगत वर्षों के प्रश्न )12videos
समुच्चय , सम्बन्ध तथा फलन
- BOOK - ARIHANT HINDICHAPTER - सम्मिश्र संख्याएँEXERCISE - प्रश्नावली (विगत वर्षों के प्रश्न )12videos
सम्मिश्र संख्याएँ
Similar Questions
यदि f:R→R एक फलन है f(2x+3)+f(2x+7)=2, ∀x∈R को सन्तुष्ट करता है, तब f(x) का आवर्त है
06:48View Solutionफलन f(x)=ex−[x]+cosax के लिए a का सम्भव मान है, जहाँ [.] एक महत्तम पूर्णांक फलन है
View Solutionयदि y= x -3 द्वारा परिभाषित R सम्बन्ध (11,12, 13 ) से (8,10,12) है, तब R−1 है
06:22View Solutionनिम्न सम्बन्ध R को कोटि 3 के वर्ग आव्यूहों पर विचारित कीजिए | R={(A,B)∣A=p−1BP, किसी व्युत्क्रमणीय आव्यूहों M तथा N के R={(A,B)∣A=P−1BP, किसी व्युत्क्रमणीय आव्यूह P के लिए }
वक्तव्य I R एक तुल्यता सम्बन्ध है
वक्तव्य II किन्ही दो व्युत्क्रमणीय 3×3 आव्यूहों M तथा N के लिए (MN)−1=N−1M−103:12View Solutionयदि z≠1 तथा z2z−1 वास्तविक है, तो z द्वारा निरूपित सम्मिश्र संख्या वाला बिन्दु
03:24View Solutiont1=(sinθ)cosθ,t2=(sinθ)sinθ,t3=(cosθ)cosθ,t4=(cosθ)sinθ (A) t3>t1>t2 (B) t4>t2>t1 (C) t4>t1>t2 (D) t1>t3>t2
05:20View SolutionThe oscillation period on the surface of a simple pendulum T_1 And oscillation period at R height from the surface T_2 , R is the radius of the earth. T_2/T_1 Its value
06:39View SolutionLet T be the set of all triangles in a plane with R a relation in T given by R={(T1,T2):T1 is congruent to T2}. Show that R is an equivalence relation.
09:25View SolutionLet T be the set of all triangles in a plane with R a relation in T given by R={(T1,T2):T1≅T2}. Show that R is an equivalence relation.
View SolutionShow that the relation R defined in the set A of all triangles as : R=[(T1,T2):T1andT2 are similar triangles} is an equivalence relation .
04:43View SolutionLet T be the set of all triangles in a plane with R a relation in T given by : R={(T1,T2):T1 is congruent to T_2}. Show that R is an equivalence relation.
02:38View SolutionShow that relation R={(T1,T2): T1 is similar to T2}, defined on the set of all triangles, is an equivalence relation.
06:14View SolutionShow that the relation R. defined in the set A of all triangle as R={(T1,T2):T1is similar to T2,is an equivalence relation. Consider three right angled triangles T1with sides 3,4,5,T2 with sides 5,12,13 and T3 with sides 6,8,10. Which triangle among T1,T2 andT3 are related ?
02:51View SolutionTime period of a simple pendulum on the surface of the earth is T1 and at a height R above the surface of the earth is T2, here R is the radius of the earth the ratio T1T2 is
03:44View SolutionShow that the points (at21,2at1)(at22,2at2) and (a,0) are collinear if t1t2=−1
01:39View Solution