The sum of n terms of an Arithmetic progression is Sn=2n2+6n. Find the first term and the common difference.Solution in Kannada
The correct Answer is:8
Step by step video, text & image solution for The sum of n terms of an Arithmetic progression is S_n=2n^2+6n. Find the first term and the common difference. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ARITHMETIC PROGRESSIONSBook:OSWAAL PUBLICATIONChapter:ARITHMETIC PROGRESSIONSExercise:LONG ANSWER TYPE QUESTION-I
Explore 11 Videos
- ARITHMETIC PROGRESSIONSBook:OSWAAL PUBLICATIONChapter:ARITHMETIC PROGRESSIONSExercise:LONG ANSWER TYPE QUESTIONS-II
Explore 13 Videos
- ARITHMETIC PROGRESSIONSBook:OSWAAL PUBLICATIONChapter:ARITHMETIC PROGRESSIONSExercise:VERY SHORT ANSWER TYPE QUESTION
Explore 8 Videos
- AREAS RELATED TO CIRCLES Book:OSWAAL PUBLICATIONChapter:AREAS RELATED TO CIRCLES Exercise:LONG ANSWER TYPE QUESTIONS - I
Explore 20 Videos
- CIRCLES Book:OSWAAL PUBLICATIONChapter:CIRCLES Exercise:TEXTBOOK CORNER (EXERCISE 4.2)
Explore 13 Videos
Similar Questions
Find the sum of all natural numbers between 200 and 300 which are divisible by 6.
View SolutionThe sum of four consecutive terms which are in an arithmetic progression is 32 and the ratio of the product of the first and the last term to the product to two middle terms is 7:15. Find the number.
View SolutionWhat is the common difference between the consecutive terms of an A.P.
View SolutionIn the given figure, AOB is a sector of angle 60∘ of a circle with centre O and radius 17 cm . If AP ⊥ OB and AP = 15 cm find the area of the shaded region.
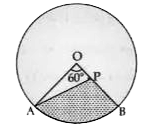
View SolutionFrom a point Q ,the length of the tangent to a circle is 24 cm and the distacne to Q from the centre is 24.5 cm.The radius of the circle is
(a) 4.92 cm
(b)12 cm
©15 cm
(d)24.5 cm
View SolutionIf the arithmetic progression whose common difference is nonzero the sum of first 3n terms is equal to the sum of next n terms. Then, find the ratio of the sum of the 2n terms to the sum of next 2n terms.
View SolutionThe sum of n terms of two arithmetic progressions are in the ratio 2n+3:6n+5, then the ratio of their 13th terms, is
View SolutionFind the first term and common difference of the Arithmetic Progressions whose nth terms are given below
tn=−3+2n
View SolutionThe sum of first n terms of an AP is given by Sn=2n2+3n. Find the common difference of the AP.
View SolutionIf the arithmetic progression whose common difference is nonzero the sum of first 3n terms is equal to the sum of next n terms. Then, find the ratio of the sum of the 2n terms to the sum of next 2n terms.
View SolutionIf the arithmetic progression whose common difference is nonzero the sum of first 3n terms is equal to the sum of next n terms. Then, find the ratio of the sum of the 2n terms to the sum of next 2n terms.
View SolutionIf the arithmetic progression whose common difference is nonzero the sum of first 3n terms is equal to the sum of next n terms. Then, find the ratio of the sum of the 2n terms to the sum of next 2n terms.
View SolutionIf the sum of the first n terms of an Arithmetic progression is Sn=nX+12n(n−1)Y where X and Y are constants, find the first term and common difference.
View SolutionThe sum of first n terms of an arithmetic sequence is n2+2n Find the common difference.
View SolutionThe sum of n terms of two arithmetic progressions are in the ratio 2n+3:6n+5, then the ratio of their 13th terms, is
View Solution