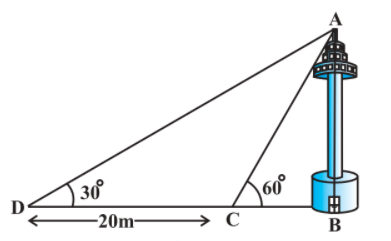
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60∘. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30∘ (see figure below). find the height of the tower and the width of the canal.
 .Solution in Kannada
.Solution in Kannada
The correct Answer is:Height of tower=10√3m.
Width of the canal=10m
Step by step video, text & image solution for A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60^(@). From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30^(@) (see figure below). find the height of the tower and the width of the canal. . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SOME APPLICATION OF TRIGONOMETRYBOOK - OSWAAL PUBLICATIONCHAPTER - SOME APPLICATION OF TRIGONOMETRYEXERCISE - LONG ASNWER TYPE QUESTIONS-II
1 Videos
- SOLVED PAPER SSLC KARNATAKA JUNE 2020 BOOK - OSWAAL PUBLICATIONCHAPTER - SOLVED PAPER SSLC KARNATAKA JUNE 2020 EXERCISE - Answer the following questions
37 Videos
- SSLC KARNATAKA TOPPERS' ANSWERS MARCH 2018 Class-XBOOK - OSWAAL PUBLICATIONCHAPTER - SSLC KARNATAKA TOPPERS' ANSWERS MARCH 2018 Class-XEXERCISE - SECTION-E
4 Videos
Similar Questions
A vertical tree is broken by the wind at a height of 6 m from its foot and its top touches the ground at a distance of 8 m from the foot of the tree. Calculate the distance between the top of the tree before breaking and the point at which of the tree touches the ground after break.
View SolutionExpress the denominator of 23/20 the form of 2n×5m and state whether the given fraction is terminating or non-terminating repeating decimal.
View SolutionSolve the equation x2−x−2=0 graphically.
View SolutionA TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60∘. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.
View SolutionA T.V. Tower stands vertically on a bank of a river. From a point on the other bank directly opposite to the tower, the angle of elevation of the top of the tower is 60 degrees. From a point 20m away this point on the same bank, the angle of elevation of the top of the tower is 30o . Find the height of the tower and the width of the river.
View SolutionA TV-tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60∘. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of tower is 30∘ (see fig.) . FInd the height of the tower and the width of the canal.
View Solutionएक नहर के एक तट पर एक टीवी टॉवर ऊर्ध्वाधर खड़ा है l टॉवर के शिखर का उनंयन कोण 60∘ है इसी तट पर इस बिंदु से 20 m दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थिति एक अन्य बिंदु से टॉवर के शिखर का उनंयन कोण 30∘ हैl ( देखिए आकृति )l टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए l
View SolutionA T.V. tower stands vertically on the side of a road. From a point on the other side directly opposite to the tower the angle of elevation of the top of tower is 60∘. From another point 10 m away from the point, on the line joining the point of the foot of the tower, the angle of elevation of the top of the tower is 30∘. THe width of the road is......
View SolutionA TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60∘. From another point 20m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30∘ (see Figure ). Find the height of the tower and the width of the canal.
View SolutionA TV tower stands verically on the bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60∘. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30∘. Find the height of the tower and the width of the canal.
View SolutionA TV tower stands vertically on a bank of a canal. The tower is watched from a point on the other bank directly opposite to it. The angle of elevation of the top of the tower is 58∘ . From another point 20m away from this point on the line joining this point to the foot of the tower , the angle of elevation of the top of the tower is 30∘. Find the height of the tower and the width of the canal . (tan58∘=1.6003)
View SolutionAt a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ The height of the tower is
View SolutionFrom a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ . The height of the tower is
View SolutionA TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60∘. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.
View SolutionA TV-tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60∘. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of tower is 30∘ (see fig.) . FInd the height of the tower and the width of the canal.
View Solution
