समीकरण y=Acos2(2πnt−2πxλ) दर्शाता है, एक तरंग
जिसका आयाम A/2, आवृत्ति 2n एवं तरंगदैर्ध्य λ/2 है
जिसका आयाम A/2, आवृत्ति 2n एवं तरंगदैर्ध्य λ है
जिसका आयाम A, आवृत्ति 2n एवं तरंगदैर्ध्य 2λ है
जिसका आयाम A, आवृत्ति n एवं तरंगदैर्ध्य λ है
The correct Answer is:D
समीकरण को पुन: लिखने पर
y=A2cos(4πnt−4πxλ)+A2
अत: आयाम =A2, आवृत्ति =ω2π=4πn2π=2n
तरंगदैर्ध्य =2πk=2π4π/λ=λ/2
Topper's Solved these Questions
Similar Questions
सूत्र X=3yz2 में X और Z क्रमश : धारिता और चुंबकीय क्षेत्र की विमाये है MKS पद्धति में Y की विमाये है
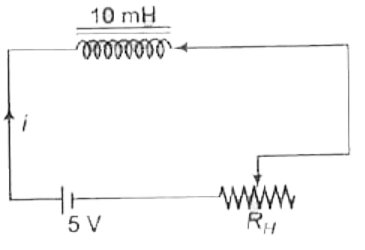
View Solutionनिम्न परिपथ का प्रतिरोध बढ़ रहा है। यदि किसी क्षण परिपथ का प्रतिरोध 10 ओम हो, तो परिपथ में धारा होगी
View SolutionThe path difference between the two waves y_(1)=a_(1) sin(omega t-(2pi x)/(lambda)) and y(2)=a_(2) cos(omega t-(2pi x)/(lambda)+phi) is
View SolutionShow that the equation y=a sin (2pi nt-(2pi)/lambda x) respresents a progressive wave of velocity C given by C=n lambda .
View SolutionIf (x)/(cos theta)=(y)/(cos(theta-(2pi)/(2)))=(2)/(cos(theta+(2pi)/(3))), then x+y+z=
View SolutionA linear SHM is represented by x=5sqrt(2) ("sin" 2pi t+ "cos" 2pi t) cm. What is the amplitude of SHM ?
View SolutionIf (x)/( cos theta ) = (y) /( cos (theta - 2pi//3))=(z)/( cos ( theta + 2pi//3)) , then x+y+z=
View Solutionसमीकरण निकाय x+y=2π3,cosx+cosy=32, जहाँ x और y वास्तविक है , के हलों का समुच्चय ………….. है।
View Solutionअन्तराल [0,2π] में समीकरण x+2tanx=π2 मूलों की संख्या है
View SolutionThe path difference between the two waves y_(1) = a_(1) sin (omega t - (2pi x)/(lambda)) and y_(2) = a_(2) cos (omega t - (2pi x)/(lambda) + phi) is ……….
View Solutiony1=a1sin(ωt−2πxλ) तथा y2=a2cos(ωt−2πxλ+ϕ) तरंगों के मध्य पथांतर ज्ञात कीजिए।
View Solutionthe equation y = A cos^(2) (2 pi nt -2 pi x/lambda) दर्शाता है, एक तरंग
View Solutiony=cos((2pi)/(lambda)x) cos(2pi vt) Whose equation is: -
View SolutionThe path difference between the two waves y_(1)=a_(1) sin(omega t-(2pi x)/(lambda)) and y(2)=a_(2) cos(omega t-(2pi x)/(lambda)+phi) is
View SolutionIf S=cos2(πn)+cos2(2πn)+....+cos2((n−1)πn), then S equals
View Solution

