आवेश Q को तीन समकेन्द्रिय तथा त्रिज्या a, b, c (a<b<c) के गोलाकार कोशों पर इस तरह वितरित किया है कि तीनों पर क्षेत्रीय आवेश घनत्व बराबर है | कोशों के केन्द्र से दूरी r(r<a) पर स्थित एक बिन्दु पर कुल विभव का मान होगा
Q4πε0(a+b+c)
Q(a+b+c)4πε0(a2+b2+c2)
Q12πε0(ab+bc+ca)abc
Q4πε0(a2+b2+c2)(a3+b3+c3)
The correct Answer is:B
P पर विभव V=kQaa+kQbb+kQcc
∵Qa:Qb:Qc::a2:b2:c2 {चूँकिσa=σb=σc}
∴Qa=[a2a2+b2+c2]Q
Qb=[b2a2+b2+c2]Q
Qc=[c2a2+b2+c2]Q
V=Q4π∈0[(a+b+c)a2+b2+c2].

Topper's Solved these Questions
- स्थिर वैद्युतBOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - Graphical Questions
13 Videos
- स्थिर वैद्युतBOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - JEE Section (More than one correct answers)
17 Videos
- स्थिर वैद्युतBOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - Ordinary Thinking (संधरित्रों का संयोजन)
91 Videos
- सरल आवर्त गति BOOK - ERRORLESS HINDICHAPTER - सरल आवर्त गति EXERCISE - Self Evaluation Test (सरल आवर्त गति )
19 Videos
Similar Questions
दिए गये परिपथ में, C के मान के 1μF से 3μF परिवर्तित होने से, 2μF संधारित्र पर आवेश Q2 में परिवर्तन होता है। के पहलन के रूप में Q2 को कौन-सा आलेख सही दर्शाता है? (आलेख केवल व्यवस्था आरेख है और स्केल के अनुसार नहीं है।)
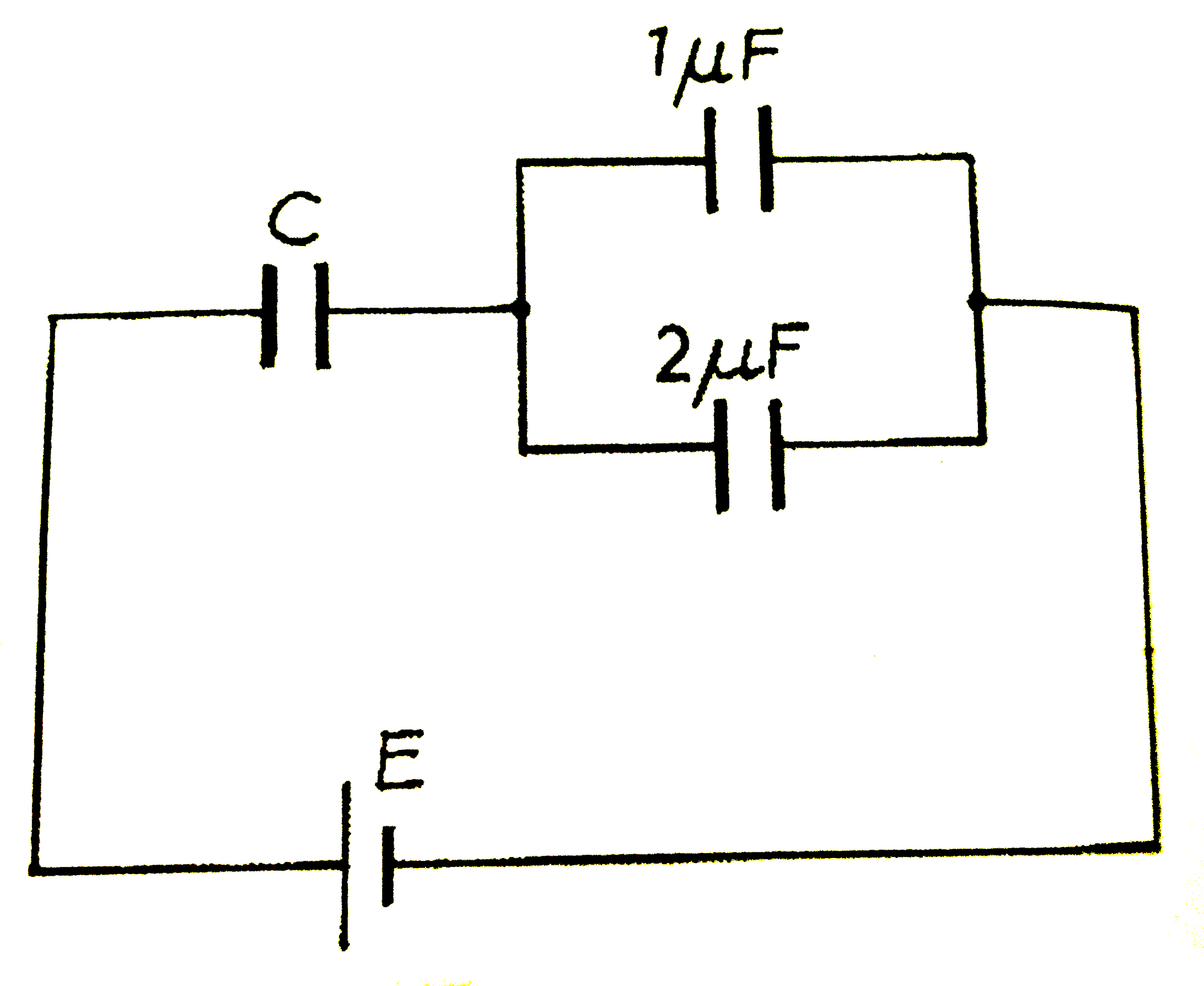
View Solutionविद्युत क्षेत्र की तीव्रता का मात्रक एवं विमा लिखिए
View Solutionसंधारित्रों से बने एक परिपथ को चित्र में दिखाया गया है| एक बिन्दु - आवेश Q ( जिसका मान 4μF तथा 9μF वाले संधारित्रों के कुल आवेशों के बराबर है ), के द्वारा 30m दूरी पर वैद्युत-क्षेत्र का परिमाण होगा
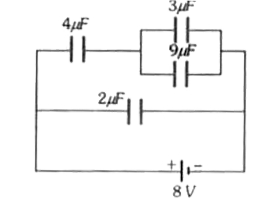
View Solutionएक सरल लोलक , का गोलक एक धात्विक खोकला गोला है। इसका आवर्तकाल T है। जब गोलक में रेत भरी है। तब आवर्तकाल T1 है जब यह मरकरी से भरा है तब आवर्तकाल T2 है जब यह मरकरी से आधा भरा है तब इसका आवर्तकाल T3 है । तब निम्न में से सही विकल्प है।
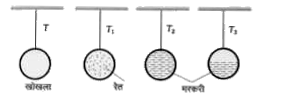
View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionमाना PQ और RS,r त्रिज्या के वृत्त के व्यास के सिरों पर खींची गई स्पर्शियाँ है। यदि PS और RQ परिधि पर स्थिति बिन्दु X पर प्रतिच्छेद करते है तो 2r बराबर है-
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionयदि बिंदु (3,4) समीकरण 3y=ax+6 के आलेख पर स्थित है , तो a का मान होगा :
View Solutionमाना की R कोई वास्तविक सँख्या का समुच्चय है। एक सक्रिया R पर इस प्रकार परिभाषित है कि a*b=a+b+2ab तो 2*3 का मान ज्ञात किया।
View Solutionसंकेंद्रित कोशों के कारण विभव | चालकों में आवेश स्थानांतरण चालकों की अर्थिंग
View Solutionदो अनन्त लम्बाई के समान्तर तार जिन पर रेखीय आवेश घनत्व क्रमश: λ1, औरλ2 , हैं R मीटर की दूरी पर रखे हैं, उनमें से किसी एक की एकांक लम्बाई पर बल होगा
View Solution(-1-1) और (4, 2) से समान दूरी पर स्थित बिन्दुओं के बिन्दुपथ का समीकरण है
View Solution
