संधारित्र की धारिता 1μF है इसे 30 V तक आवेशित करके बैट्री से पृथक कर दिया जाता है | यदि इसे 2μF संधारित्र से जोड़ा जाए, तब इस निकाय द्वारा ऊर्जा क्षय होगी
300μJ
450μJ
225μJ
150μJ
The correct Answer is:A
प्रारम्भिक ऊर्जा =12×1×10−6×(30)2=450×10−6J.
अंतिम ऊर्जा =12(C1+C2)V2common[∵V=V1C1+V2C2C1+C2]
=12×3×10−6×(10)2=150×10−6J
ऊर्जा क्षय =(450−150)×10−6J=300×10−6J=300μJ.
Topper's Solved these Questions
- स्थिर वैद्युतBook:ERRORLESS HINDIChapter:स्थिर वैद्युतExercise:Ordinary Thinking (संधरित्रों का संयोजन)
Explore 91 Videos
- स्थिर वैद्युतBook:ERRORLESS HINDIChapter:स्थिर वैद्युतExercise:Critical Thinking
Explore 109 Videos
- स्थिर वैद्युतBook:ERRORLESS HINDIChapter:स्थिर वैद्युतExercise:Ordinary Thinking (विद्युत फ्लक्स एवं गॉस नियम)
Explore 37 Videos
- सरल आवर्त गति Book:ERRORLESS HINDIChapter:सरल आवर्त गति Exercise:Self Evaluation Test (सरल आवर्त गति )
Explore 19 Videos
Similar Questions
संधारित्रों से बने एक परिपथ को चित्र में दिखाया गया है| एक बिन्दु - आवेश Q ( जिसका मान 4μF तथा 9μF वाले संधारित्रों के कुल आवेशों के बराबर है ), के द्वारा 30m दूरी पर वैद्युत-क्षेत्र का परिमाण होगा
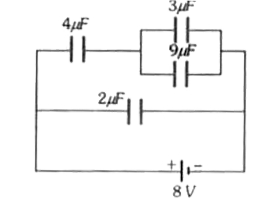
View Solutionदो समान ऋण आवेश q , q, Y- अक्ष पर बिन्दुओं (0 , a) तथा (0 , -a) पर स्थित हैं | एक धन आवेश Q, X- अक्ष पर बिन्दु (2a, 0 ) पर विरामावस्था से मुक्त किया जाता है | आवेश Q
View SolutionR त्रिज्या तथा L लम्बाई के एक बेलन को एकसमान वैद्युत क्षेत्र E के अनुदिश अक्ष में रखा गया है , तो बेलन के पृष्ठ से सम्पूर्ण फ्लक्स हेतु व्यंजक
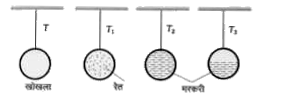
View Solutionएक सरल लोलक , का गोलक एक धात्विक खोकला गोला है। इसका आवर्तकाल T है। जब गोलक में रेत भरी है। तब आवर्तकाल T1 है जब यह मरकरी से भरा है तब आवर्तकाल T2 है जब यह मरकरी से आधा भरा है तब इसका आवर्तकाल T3 है । तब निम्न में से सही विकल्प है।
View Solutionआवेशित चालक की ऊर्जा | संधारित्र में संचित ऊर्जा
View Solutionसमान्तर-प्लेट संधारित्र की धारिता
View Solutionआवेशित चालक की स्थितिज ऊर्जा || आवेशित संधारित्र की स्थितिज ऊर्जा
View Solutionचालक तथा संधारित्र की धारिता
View Solutionचालक तथा संधारित्र की धारिता
View Solutionआवेशित संधारित्र में संग्रहीत ऊर्जा
View SolutionRecap|संधारित्र की धारिता |समांतर प्लेट संधारित्र |OMR|Summary
View SolutionRecap|आवेशित चालक की ऊर्जा |संधारित्र की ऊर्जा |OMR|Summary
View Solutionधारिता|संधारित्र का सिद्धांत|आवेशित संधारित्र में संचित ऊर्जा|गोलीय संधारित्र की धारिता|OMR|Summary
View Solutionसंधारित्र का सिद्धांत #!#संधारित्र की ऊर्जा
View Solutionआवेशित संधारित्र में संचित ऊर्जा|समांतर प्लेट संधारित्र|गोलीय संधारित्र की धारिता|OMR|Summary
View Solutionगोलीय संधारित्र की धारिता |प्रश्न |सर्वसम आवेशित छोटी बूंदों को मिलाना |ऊर्जा घनत्व |प्रश्न |OMR|Summary
View Solution

