1gm द्रव्यमान तथा 10−8C आवेश की एक गेंद को बिन्दु A जिस पर 600 V विभव है से बिन्दु B जिस पर विभव शून्य है तक ले जाया जाता है | बिन्दु B पर गेंद का वेग 20 सेमी./सैकण्ड है | बिन्दु A पर गेंद का वेग होगा
22.8 सेमी./सैकण्ड
228 सेमी./सैकण्ड
16.8 सेमी./सैकण्ड
168 सेमी./सैकण्ड
The correct Answer is:A
12m(v21−v22)=QV
⇒12×10−3{v21−(0.2)2}=10−8(600−0)
⇒v1=22.8cm/s
Topper's Solved these Questions
- स्थिर वैद्युतBook:ERRORLESS HINDIChapter:स्थिर वैद्युतExercise:Ordinary Thinking (वैद्युत द्विध्रुव)
Explore 43 Videos
- स्थिर वैद्युतBook:ERRORLESS HINDIChapter:स्थिर वैद्युतExercise:Ordinary Thinking (विद्युत फ्लक्स एवं गॉस नियम)
Explore 37 Videos
- स्थिर वैद्युतBook:ERRORLESS HINDIChapter:स्थिर वैद्युतExercise:Self Evaluation Test
Explore 8 Videos
- सरल आवर्त गति Book:ERRORLESS HINDIChapter:सरल आवर्त गति Exercise:Self Evaluation Test (सरल आवर्त गति )
Explore 19 Videos
Similar Questions
निरक्षीय समतल में किसी बिन्दु पर द्विध्रव आघूर्ण एवं विद्युत क्षेत्र के बीच कोण होगा
View SolutionR त्रिज्या तथा L लम्बाई के एक बेलन को एकसमान वैद्युत क्षेत्र E के अनुदिश अक्ष में रखा गया है , तो बेलन के पृष्ठ से सम्पूर्ण फ्लक्स हेतु व्यंजक
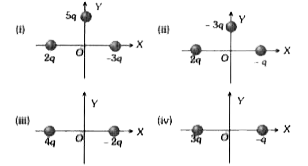
View Solutionनिम्न चार स्थितियों में आवेशित कण मूल बिंदु से बराबर - बराबर दूरियों पर स्थित हैं मूल बिंदु क्षेत्र के परिमाण को अधिकतम पहले लेते हुये इन्हें व्यवस्थित करें
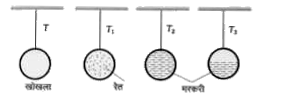
View Solutionएक सरल लोलक , का गोलक एक धात्विक खोकला गोला है। इसका आवर्तकाल T है। जब गोलक में रेत भरी है। तब आवर्तकाल T1 है जब यह मरकरी से भरा है तब आवर्तकाल T2 है जब यह मरकरी से आधा भरा है तब इसका आवर्तकाल T3 है । तब निम्न में से सही विकल्प है।
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionकोई फलन किसी बिन्दु x = a पर अवकलनीय कहलता है, जब -
View Solutionकिसी बिन्दु पर संतत फलन होता है -
View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
View Solutionबिन्दु (-1,0) से होकर जाने वाले और y-अक्ष को (0,2) पर स्पर्श करने वाला वृत्त निम्न बिन्दु से भी होकर जाता है ।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionपरवलय y2=4ax के बिन्दु (a4,a) पर अभिलम्ब का समीकरण है
View Solution

