Question

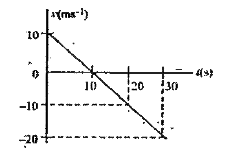
A particle of mass 1 g moves on a straight line. The variation of its velocity with time is shown in fig. Find the force acting on the particle att = 1 s,4s and 7 s.

Explanation

(i) At t =1 s, acceleration of the particle is equal to the slope of the straight line from 0 to 3s as 1 s is between 0 and 3 s. Acceleration of the particle at t = 1s is
`a=(v_(f)-v_(i))/(t_(f)-t_(i)) = (15-0)/(3-0) = 5ms^(-2)`
`therefore` Force acting on the particle
`= ma = 1 xx 10^(-3) xx 5 = 5 xx 10^(-3) N`
(ii) At t= 4s, acceleration is given by
a= slope of the straight line from t= 3 to 5s
`=(v_(f)-v_(i))/(t_(f)-t_(i)) = (15-5)/(5-3) = 0/2 ms^(-2)`
`therefore` Force acting on the particle
`=ma = 1 xx 10^(-3) xx 0 = 0 N`
(iii) At t= 7s, acceleration is given by
a= slope fo the straight line from t = 5 to 8s
`=(v_(f)-v_(i))/(t_(f)-t_(i)) = (0-15)/(8-5) = 15/3 = 5 ms^(-1)`
`therefore` Force acting on the particle
`=ma = 1 xx 10^(-3) xx -5 =-5 xx 10^(-3) N`
Negative sign indicates that the force is in the opposite direction of the motion of the particle.