Three vectors →A,→B,→C are shown in the figure angle between (i) →Aand→B(ii)→Band→C,(iii)→Aand→C
 Solution in Telugu
Solution in Telugu
To find the angle between two vectors we connect the tails of the two vectors. We can shift the vectors parallel to themselves such that tails of A, B and are connected as shown in figure.
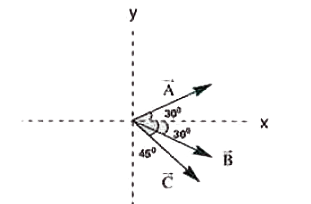
Now we observe that angle between →Aand→B is 60∘ B and C is 15∘ and between →Aand→C is 75∘
Topper's Solved these Questions
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:EXERCISE-A (Vectors & Scalars)
Explore 25 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:EXERCISE-A (Addition & Subtractions of Vectors)
Explore 10 Videos
- MAGNETISMBook:AAKASH SERIESChapter:MAGNETISMExercise:PROBLEMS (LEVEL-II)
Explore 13 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:QUESTION FOR DESCRIPTIVE ANSWER
Explore 7 Videos
Similar Questions
In Latin, the word vector means
View SolutionThe resultant of two forces cannot exceed
View SolutionThe force between the two poles is reduced to 'x' newtons when their separation is increased n times. It is increased by 'y' newtons when their separation is made 1/nth of their original value. What is the relation between x and y?
View SolutionA particle is projected over a triangle from one end of a horizontal base and garzing the vertex falls on the other end of the base . If α and β the base angles and θ the angle of projection then show that tanθ=tanα+tanβ.
View SolutionThree vectors vecA,vecB,vecC are shown in the figure. Find angle between (i) vecA and vecB (ii) vecB and vecC (iii) vecA and vecC .
View Solution→A,→Band→C are vectors such that →C=→A+→Band→C⊥→A and also C= A . Angle between →Aand→B is :
View SolutionIf →a,→band→c are three vectors such that →a×→b=→c,→b×→c=→a,→c×→a=→b then prove that |→a|=∣∣→b∣∣=|→c|
View SolutionIf →a,→band→c are three vectors such that →a×→b=→c,→b×→c=→a,→c×→a=→b then prove that |→a|=∣∣→b∣∣=|→c|
View SolutionLet →a,→b,→c be three vectors such that
→a⊥(→b+→c),→b⊥(→c+→a)and→c⊥(→a+→b), if |→a|=1,∣∣→b∣∣=2,
|→c|=3, then ∣∣→a+→b+→c∣∣ is,
View Solutionसिद्ध करें कि
(i) [→a+→b →b+→c →c+→a]=2[→a →b →c]
(ii) →a+→b,→b+→c और →c+→a असमतलीय होगें यदि →a,→b,→c तीन असमतलीय सदिश हों ।
View SolutionVectors vecA,vecB and vecC are shown in figure. Find angle between (i) vecA and vecB " " (ii) vecA and vecC" " (iii) vecB and vecC .
View SolutionIf →a , →b , →c are three vectors, prove that [→a+→c,→a+→b,→a+→b+→c]=−[→a,→b,→c]
View SolutionThree vectors →A,→B,→C are shown in the figure angle between (i) →Aand→B(ii)→Band→C,(iii)→Aand→C

View SolutionThree vectors →A,→B,→C are shown in the figure angle between (i) →Aand→B(ii)→Band→C,(iii)→Aand→C

View SolutionIf →a,→band→c are three vectors such that →a×→b=→c,→b×→c=→a,→c×→a=→b then prove that |→a|=∣∣→b∣∣=|→c|
View Solution