IF →A×→B=→C×→Dand→A×→C=→B×→D+ while ∣∣→A∣∣≠∣∣→D∣∣∣∣→B∣∣≠∣∣→C∣∣ show (→A−→D) that and (→B−→C) are parallel Solution in Telugu
Given
→A×→B=→C×→D
→A×→C=→B×→D
subtracting (2) from (1) we get
→A×→B−→A×→B−→A×→C=→C×→D−→B×→D
∴→A×(→B−→C)
=(→C−→B)×→D[∴→P×(→Q+→R)=→P×→Q+→P×→R]
∴→A×(→B−→C)=−(→B−→C)×→D∴→A×(→B−→C)×→D=0∴→A×→B−→C)−→D×(→B−→C)=0
[∴P→A−→D)×(→B−→C)=0
Now ∣∣→A∣∣≠∣∣→D∣∣and∣∣→B∣∣≠∣∣→C∣∣
∴(→A−→D)≠0and(→B−→C)≠0
(→A−→D)and(→B−→C) are at an angle 0∘or(→A−→D)and(→B−→C) are parallel
[,.→P×→Q=PQsinθandP≠0≠Q hence sin θ=0]
Topper's Solved these Questions
- ELEMENTS OF VECTORSBook:AAKASH SERIESChapter:ELEMENTS OF VECTORSExercise:LONG ANSWER TYPE QUESTIONS
Explore 5 Videos
- ELEMENTS OF VECTORSBook:AAKASH SERIESChapter:ELEMENTS OF VECTORSExercise:SHORT ANSWER TYPE QUESTIONS
Explore 9 Videos
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
Explore 4 Videos
- GEOMETRICAL OPTICSBook:AAKASH SERIESChapter:GEOMETRICAL OPTICSExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
Explore 6 Videos
Similar Questions
State parallelogram law of vectors . Derive an expression for the magnitude and direction of the resultant vector .
View SolutionState and prove the parallelogram law of vectors.
View SolutionFour identical point charges are fixed at the four corners of a square of a side length l. Another charged particle of mass m and charge +q is projected towards centre of square from a large, distance along the line perpendicular to plane of square. The minimum value of initial velocity V0 in m/s required to cross the square is? (m=1gm.l=4√2m,Q=1μc,q=0.5μc)
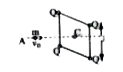
View SolutionA fish is at a depth of 12 cm in water is viewed by an observer on the bank of a lake. To what height the image of the fish is raised in cm ?
View SolutionShow that: (→a−→d)×(→b−→c)+(→b−→d)×(→c−→a)+(→c−→d)×(→a−→b) is independent of →d.
View SolutionIf →a,→b,→cand→d ar distinct vectors such that →a×→c=→b×→dand→a×→b=→c×→d. Prove that (→a−→d).(→c−→b)≠0,i.e.,→a.→b+→d.→c≠→d.→b+→a.→c.
View SolutionGiven that →a,→c,→d are coplanar the value of (→a+→d).{→a×[→b×(→c×→a)]} is:
View SolutionFor any four vectors →a,→b,→c,→d the expressions (→b×→c).(→a×→d)+(→c×→a).(→b×→d)+(→a×→b).(→c×→d)is always equal to:
View SolutionGiven →a⋅→c=4,→a⋅→d=3,→b⋅→c=2,→b⋅→d=3. Then value of (→a×→b)⋅(→c×→d) is :
View SolutionShow that (→a×→b)⋅(→c×→d)+(→b×→c)⋅(→a×→d)+(→c×→a)⋅(→b×→d)=0.
View Solution(→b×→c)⋅(→d×→a)−(→c×→d)⋅(→a×→b)−(→d×→a)⋅(→b×→c)−(→a×→b)⋅(→c×→d) बराबर है
View Solutionयदि →a व →b समान्तर हैं, तब (→a×→b)×(→c×→d)+(→a×→c)×(→b×→d) का मान है
View SolutionFor any four vectors →a , →b , →c , →d we have (→a×→b)×(→c×→d)=[→a,→b,→d]→c−[→a,→b,→c]→d=[→a,→c,→d]→b−[→b,→c,→d]→a .
View SolutionIf →a=ˆi−ˆj , →b=ˆi−ˆj−4ˆk , →c=3ˆj−ˆk and →d=2ˆi+5ˆj+ˆk , verify that
(i) (→a×→b)×(→c×→d)=[→a,→b,→d]→c−[→a,→b,→c]→d
(ii) (→a×→b)×(→c×→d)=[→a,→c,→d]→b−[→b,→c,→d]→a
View SolutionIf →a,→b,→cand→d are unit vectors such that (→a×→b).(→c×→d)=1and→a.Ve=12 then :
View Solution

