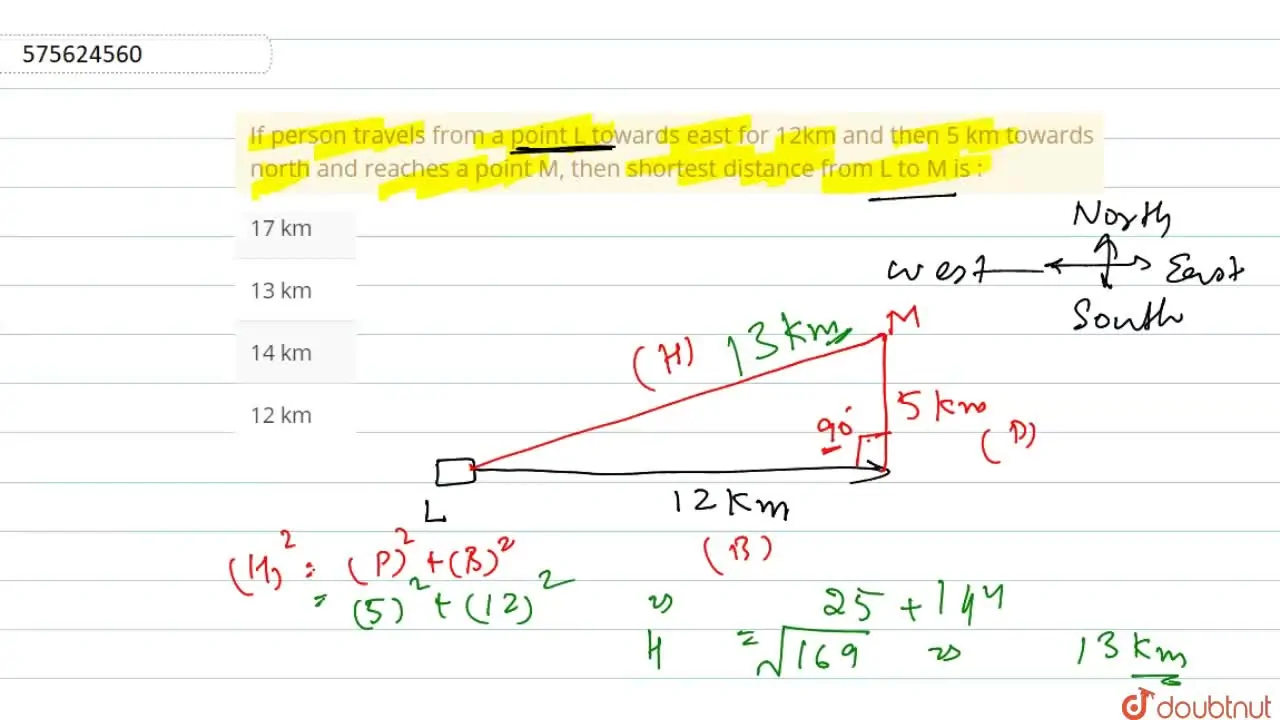
If person travels from a point L towards east for 12km and then 5 km towards north and reaches a point M, then shortest distance from L to M is :
17 km
13 km
14 km
12 km
The correct Answer is:B
Step by step video, text & image solution for If person travels from a point L towards east for 12km and then 5 km towards north and reaches a point M, then shortest distance from L to M is : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Similar Questions
If a person travels from a point L towards east for 12 km and then travels 5 km towards north and reaches a point M, then shortest distance from L to M is:
यदि एक व्यक्ति बिन्दु L से पूर्व की ओर 12 किमी. और फिर उत्तर की ओर 6 किमी, यात्रा करता है तो बिन्दु M पर पहुँचता है, तो L से M की न्यूनतम दूरी हैView SolutionA cyclist starting from point X travels straight towards east for 3 km and then turns right and covers 4 km and reaches point Y. What is the shortest distance point X and Y?
View SolutionA partical moves 5M towards east and then 12m towards north. Find the displacement and distance covered.
View SolutionA person travels 7 km eastwards and then turns right and travels 3 km and further turns right and travels 13 km. What is the shortest distance of the present position of the person from his starting point?
View SolutionFrom a starting point A, Rahul walks 3/4 km towards east and then 6/7 km towards west to reach point C.
How much more distance he travelled towards west than east ?View SolutionMr. X starts from point ‘A’ travels 80 km towards west, takes a left turn, travels 50 km and reached point ‘B’. What is the shortest distance between points ‘A’ and ‘B’?
View SolutionA man travels on a bicycle, 10 km east from the starting point A to reach point B, then the cycles 15 km south to reach point C. Find the shortest distance between A and C.
View SolutionA person moves towards East for 3 m, then towards North for 4 m and then moves vertically up by 5 m. What is his distance now from the starting point ?
View SolutionMr X runs a marathon starting from the point A he runs 5 km towards north and reach point B, then turns right runs 6 km reach point C, then turn right runs 8 km and reach point D, then turns right runs 10 km and reach point E, then turns right runs 6 km and reach point F, then turns right runs 1 km and reach point G, then turn rights runs 3 km and reach point H.
The shortest distance between point D and G is ?View SolutionA man walks 6 km towards north and turns left and walks 2 kms towards West. If he has started from point Z and reached point A, then what is the shortest distance between point Z and A
View Solution