If the number of vertices, edges and faces of a rectangular parallelopiped are denote by v,e and frespectively , the value of (v−e+f) is
0
2
4
1
The correct Answer is:B
To solve the problem, we need to determine the values of the number of vertices (V), edges (E), and faces (F) of a rectangular parallelepiped.
1. Identify the number of vertices (V):
- A rectangular parallelepiped has 8 vertices. These are the corners of the shape.
- Therefore, V=8.
2. Identify the number of edges (E):
- A rectangular parallelepiped has 12 edges. These are the line segments connecting the vertices.
- Therefore, E=12.
3. Identify the number of faces (F):
- A rectangular parallelepiped has 6 faces. These are the flat surfaces that make up the shape.
- Therefore, F=6.
4. Substitute the values into the expression V−E+F:
- We substitute the values we found into the expression:
V−E+F=8−12+6
5. Calculate the result:
- First, calculate 8−12:
8−12=−4
- Then add 6:
−4+6=2
6. Final result:
- The value of V−E+F is 2.
Conclusion:
Thus, the value of (V−E+F) for a rectangular parallelepiped is 2.
- A rectangular parallelepiped has 8 vertices. These are the corners of the shape.
- Therefore, V=8.
- A rectangular parallelepiped has 12 edges. These are the line segments connecting the vertices.
- Therefore, E=12.
- A rectangular parallelepiped has 6 faces. These are the flat surfaces that make up the shape.
- Therefore, F=6.
- We substitute the values we found into the expression:
V−E+F=8−12+6
- First, calculate 8−12:
8−12=−4
- Then add 6:
−4+6=2
- The value of V−E+F is 2.
Thus, the value of (V−E+F) for a rectangular parallelepiped is 2.
Similar Questions
Knowledge Check
If the number of vertices , edges and faces of a rectangular parllelopiped are denoted by v, e and f respectively, the value of (v−e+f)is
A0B2C4D1The number of vertices, edges and faces respectively of a cuboid are
A8, 6, 12B12, 8, 6C8, 12, 6D12, 6,8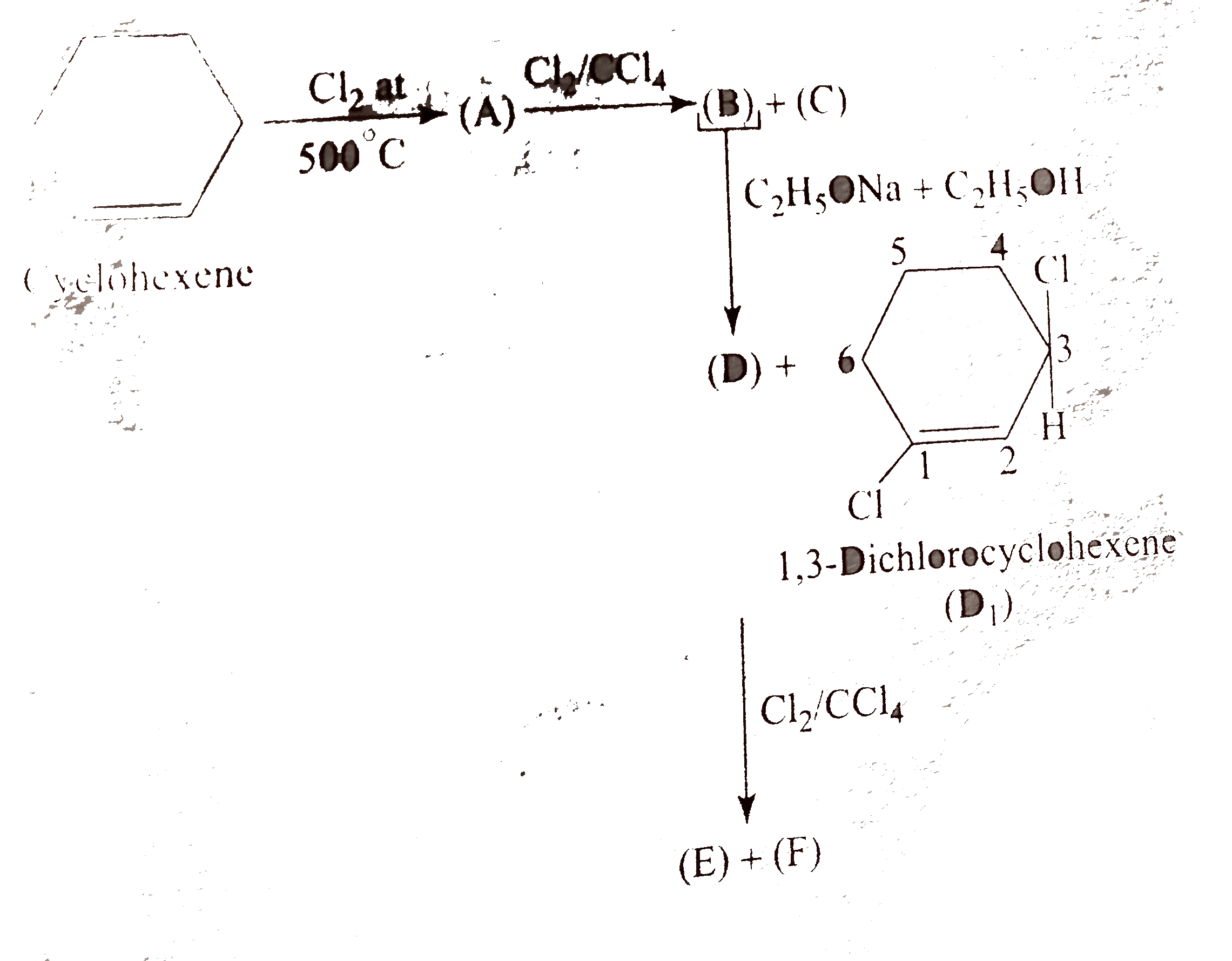
(E) and (F), respectively, are :A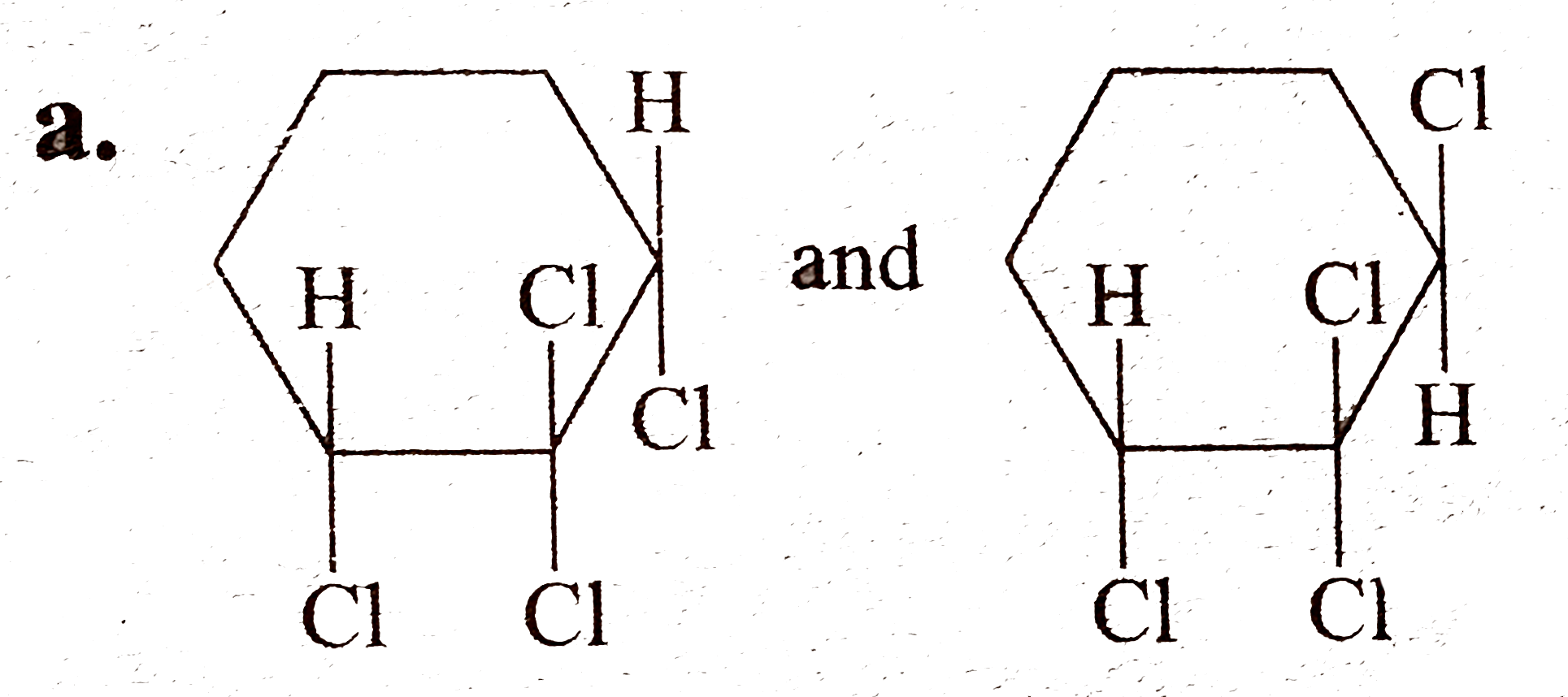 B
B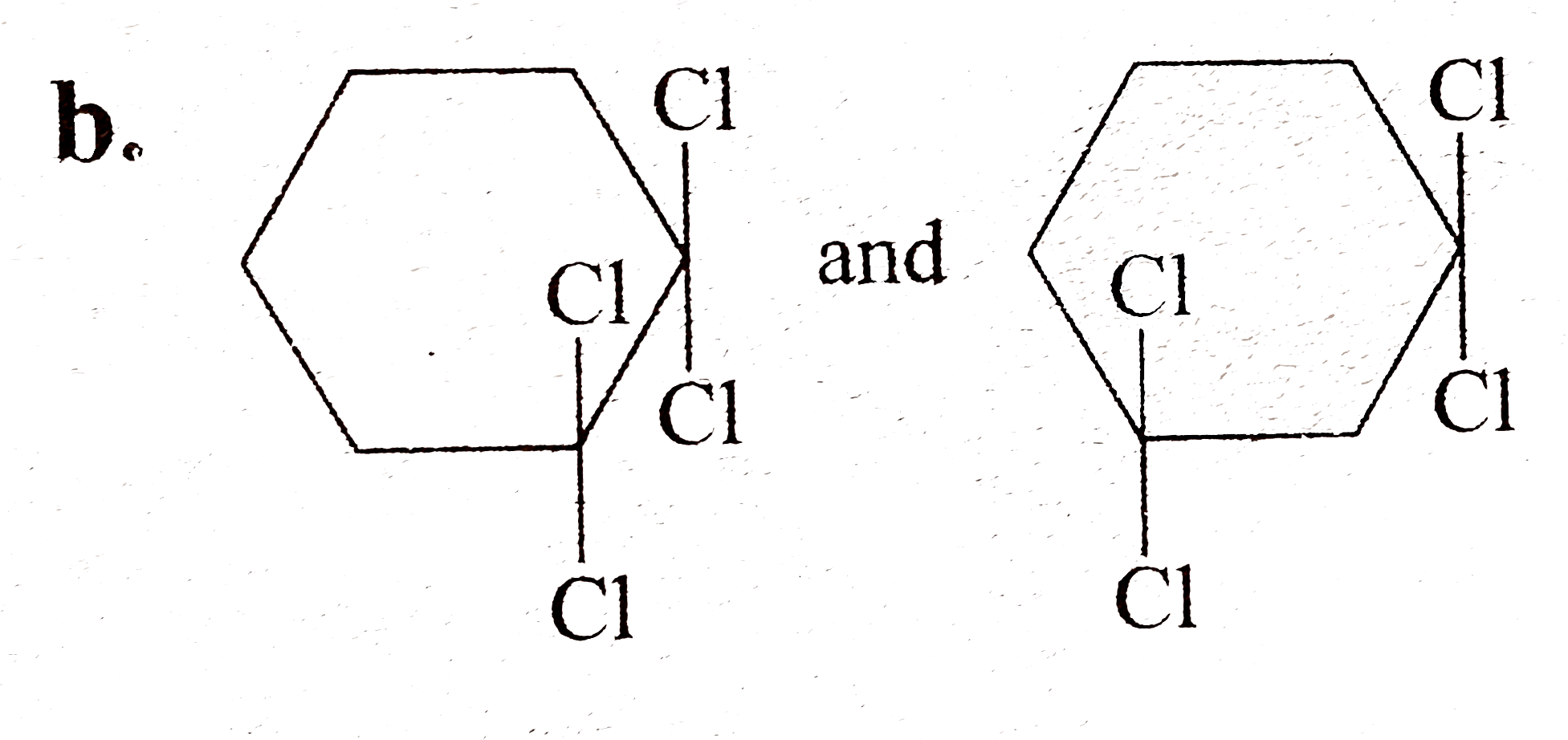 C
C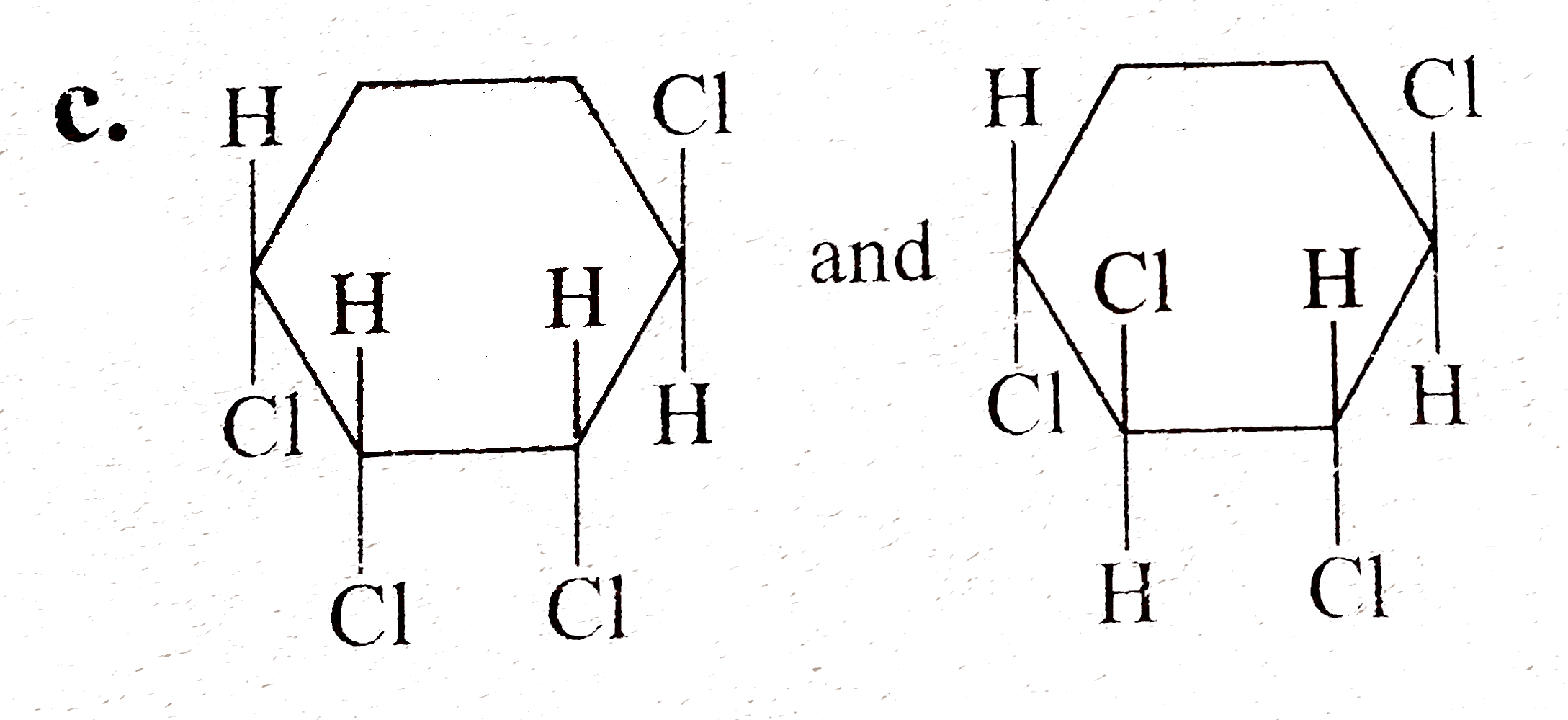 D
D
Number of vertices, edges and faces respectively in the given figure are:

View SolutionDetermine the number of edges, vertices and faces in the fig.
View SolutionIf f, e, and v represent the number of rectangular faces, number of edges and number of vertices repectively of a cuboid, then the values of f, e, and v respectively are _________.
View SolutionIf a, b and c are respectively the number of faces, edges and vertices of a pentagonal pyramid, then the value of (a+b+c2)2 - 2 is
View SolutionIf a, b and c are respectively the number of faces, edges and vertices of a pentagonal pyramid, then the value of (a+b+c2) - 12 is
View Solution
