Question

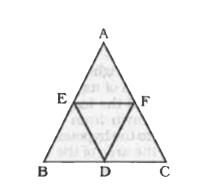
If D, E and F are the mid points of BC, CA and AB respectively of the $△ABC$ then the ratio of aria parallelogram DEFB and area of the trapezium CAFD is ,

Options

A. `2 : 3`
B. `3 : 4`
C. `1 : 2`
D. `1 : 3`

Answer

A

Explanation

To find the ratio of the area of parallelogram DEFB to the area of trapezium CAFD in triangle ABC, we can follow these steps:

Step 1: Understand the Triangle and Midpoints
Let triangle ABC have vertices A, B, and C. The midpoints of sides BC, CA, and AB are D, E, and F respectively.

Step 2: Identify Areas of Smaller Shapes
When we connect the midpoints, we form smaller triangles and a parallelogram within triangle ABC. The triangles formed are AEF, BDF, and CDE. The area of triangle ABC can be divided into four smaller areas: triangle AEF, triangle BDF, triangle CDE, and parallelogram DEFB.

Step 3: Calculate Areas of Smaller Triangles
Since D, E, and F are midpoints, each of the triangles AEF, BDF, and CDE will have equal areas. Let the area of each of these triangles be x. Therefore, the area of triangle ABC is:
\( \text{Area of } ABC = AEF + BDF + CDE = x + x + x = 3x \)

Step 4: Area of Parallelogram DEFB
The area of parallelogram DEFB can be calculated as follows:
\( \text{Area of } DEFB = \text{Area of } ABC - (\text{Area of } AEF + \text{Area of } CDE) = 3x - (x + x) = 3x - 2x = x \)

Step 5: Area of Trapezium CAFD
The area of trapezium CAFD can be calculated as:
\( \text{Area of } CAFD = \text{Area of } ABC - \text{Area of } BDF = 3x - x = 2x \)

Step 6: Calculate the Ratio
Now, we can find the ratio of the area of parallelogram DEFB to the area of trapezium CAFD:
\( \text{Ratio} = \frac{\text{Area of } DEFB}{\text{Area of } CAFD} = \frac{x}{2x} = \frac{1}{2} \)

Conclusion
Thus, the ratio of the area of parallelogram DEFB to the area of trapezium CAFD is \( \frac{1}{2} \).