यदि बल नियतांक क्रमशः k1 एवं k2 वाली दो कमानियाँ , S1 एवं S2 एकसमान बल से तनित की जाये , तब यह पाया जाता है , कि कमानी S1 पर कमानी S2 के मुकाबले अधिक कार्य किया जाता है।
प्रकथन 1 यदि कामनियाँ एकसमान मात्रा से तनित कि जाती हैं , तब S1 पर किया गया कार्य S2 पर किए गए कार्य से अधिक है।
प्रकथन 2 k1<k2
प्रकथन 1 गलत है , प्रकथन 2 सही है
प्रकथन 1 सही है , प्रकथन 2 गलत है
प्रकथन 1 सही है , प्रकथन 2 सही है , प्रकथन 2 , प्रकथन 1 कि सही व्याख्या करता है
प्रकथन 1 सही है प्रकथन 2 सही है , प्रकथन 2 , प्रकथन 1 कि सही व्याख्या नहीं करती है
The correct Answer is:A
चूँकि प्रश्न में k1 व् k2 के बीच कोई सम्बन्ध नहीं किया गया है। अतः प्रकथन 1 के बारे में कुछ भी नहीं कहा जा सकता । किन्तु प्रकथन 2 में k1<k2 अतः समान बल के लिए
W=F.x=F.Fk=F2k
⇒W∝1k
अर्थात W1>W2
किन्तु समान विस्थापन के लिए
W=F.x=12kx.=12kx2
⇒W∝k अतः W1<W2
अतः प्रकथन 2 के अनुसार , प्रकथन 1 असत्य है।
Topper's Solved these Questions
Similar Questions
दोनों सिरों पर खुली एक बेलनाकार नली की वायु में मूल आवृत्ति f है। नली को पानी में ऊर्ध्वाधर इस प्रकार डुबोया जाता है कि यह आधी पानी में रहे। वायु-स्तम्भ की मूल आवृत्ति अब है :
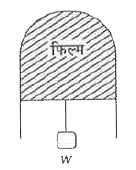
View Solutionएक U आकार के तार एवं हल्के दर्पण के बीच बनी एक पतली द्रव की फिल्म 1.5×10−2 न्यूटन के भार को आधारित करती है( चित्र में देखने) दर्पण की लम्बाई 30 सेमी है ओर इसका भार नगण्य है। द्रव की फिल्म का पृष्ट तनाव है।
View SolutionIf S1,S2,S3 be respectively the sums of n,2n,3n terms of a G.P., then prove that (S1)2+(S2)2=S1(S2+S3) .
View SolutionLet S_(1),S_(2),...,S_(101) be consecutive terms of an AP.If (1)/(S_(1)S_(2))+(1)/(S_(2)S_(3))+...+(1)/(S_(100)S_(101))=(1)/(6) and S_(1)S_(101)=50 then |S-S_(101)| is equal to
View SolutionIf S1,S2,S3be respectively the sum of n,2n and 3n terms of a GP, then S1(S3−S2)(S2−S1)2 is equal to
View Solutionयदि गु० श्रे० के n,2n,3n पदों का योग क्रमशः S1,S2,S3 हों तो सिद्ध करें की S21+S22=S1(S2+S3).
View Solutionमाना Sk=1+2+3+…+kk है। यदि S21+S22+….S210=512A है, तो A बराबर है
View Solutionएकसमान विद्युत् क्षेत्र में द्विध्रुव पर बल युग्म द्विध्रुव को घुमाने में किया गया कार्य
View SolutionIf α,β are the roots of x2+x+1=0, and sn=αn+βn, then ∣∣ ∣∣31+S11+S21+S11+S21+S31+S21+S31+S4∣∣ ∣∣=?
View SolutionLet S1,S2,......S101 be consecutive terms of A.P. If 1S1S2+1S2S3+......+1S100S101=16 and S1+S101=50, then |S1−S101| is equal to
View SolutionIf S1,S2andS3 be respectively the sum of n, 2n and 3n terms of a G.P. Prove that S1(S3−S2)=(S2−S1)2.
View SolutionIf S1,S2,S3be respectively the sum of n, 2n and 3n terms of a GP, then S1(S3−S2)(S2−S1)2 is equal to
View Solutionघर्षण बल के द्वारा किया गया कार्य
View Solutionपरिवर्ती बल के द्वारा किया गया कार्य
View Solutionस्प्रिंग बल के द्वारा किया गया कार्य
View Solutionयदि किसी भिन्न का अंश, हर से 2 कम है और यदि हर में 1 जोडा जाए तो यह 12 हो जाता है तब वह भिन्न होगी ?
View Solution
