∫dx√2ax−x2=axsin−1(xα−1),x का मान है
आप विमीय विश्लेषण द्वारा इस प्रश्न को हल करें।
0
−1
1
इनमें से कोई नहीं
The correct Answer is:A
त्रिकोणमितीय फलन विमाहिन होते हैं |
इसलिए, xa = विमाहिन
अत: a की विमा x की विमा है |
RHS की विमा =xa की विमा = विमाहिन
तथा ax= विमाहिन
x=0
Topper's Solved these Questions
- भौतिकी तथा मापन BOOK - ARIHANT HINDICHAPTER - भौतिकी तथा मापन EXERCISE - प्रश्नावली स्तर 1 (त्रुटि और मापन)
31 Videos
- भौतिकी तथा मापन BOOK - ARIHANT HINDICHAPTER - भौतिकी तथा मापन EXERCISE - प्रश्नावली स्तर 2 (केवल एक विकल्प सही है)
26 Videos
- भौतिकी तथा मापन BOOK - ARIHANT HINDICHAPTER - भौतिकी तथा मापन EXERCISE - प्रश्नावली स्तर 2 विगत वर्षों के प्रश्न
20 Videos
- प्रैक्टिस सेट 3 BOOK - ARIHANT HINDICHAPTER - प्रैक्टिस सेट 3 EXERCISE - MCQS
30 Videos
- मापन BOOK - ARIHANT HINDICHAPTER - मापन EXERCISE - परीक्षा की तैयारी हेतु प्रश्नावली (लक्ष्य JEE MAIN )(विगत वर्षा के प्रश्न )
13 Videos
Similar Questions
यदि x=α−b, तब x के मापन में महत्तम त्रुटि होगी
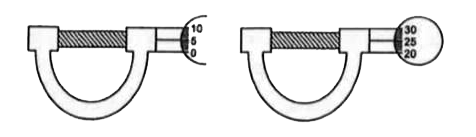
View Solutionदिखाए गए पेंचमापी में 50 वृत्तीय भाग (खाने) हैं। यह एक चक्कर में मुख्य पैमाने पर 0.5 मिमी घूमता है। गेंद का व्यास है
View Solutionएक प्रयोग में एक यंत्र से कोण मापते हैं, मुख्य पैमाने के 29 खाने वर्नियर पैमाने के 30 खानों के समान (बराबर) हैं। यदि मुख्य पैमाने का सबसे छोटा खाना 0.5∘ है, तब यंत्र का अल्पतमांक है
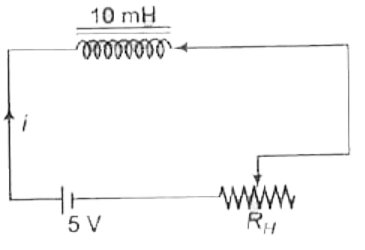
View Solutionनिम्न परिपथ का प्रतिरोध बढ़ रहा है। यदि किसी क्षण परिपथ का प्रतिरोध 10 ओम हो, तो परिपथ में धारा होगी
View Solutionएक प्रिज्म का कोण नापने में प्रयोग किया गया स्पेक्टरोमीटर निम्नलिखित मापन देता है
मुख्य स्केल मापन = 58.5 डिग्री
वर्नियर स्केल मापन = 09 भाग
दिया है- मुख्य स्केल का एक भाग 0.5 डिग्री के बराबर है।
वर्नियर स्केल पर कुल भाग 30 है और यह मुख्य स्केल के 29 भागों से मिलते हैं। उपरोक्त आँकड़ों से प्रिज्म का कोण है
View SolutionFind ∫xsin−1x√1−x2dx
View SolutionIn the equation ∫dx√2ax−x2=a2sin−1[xa−1]. Find the value of n .
View SolutionIf ∫1√2ax−x2dx=fog(x)+C , then
View Solution∫x+Sin−1x√1−x2=dx
View Solution∫sin−1x√1+xdx का मान है :
View Solution∫dx(x−3)√(x+1) का मान होगा :
View Solution∫21dx(x+1)√x2−1 का मान है :
View Solutionसमीकरण (x2+1)dydx=1 का हल है -
View Solutionमाना y=y(x), अवकल समीकरण (x2+1)2dydx+2x(x2+1)y=1 का हल है, जबकि y(0) = 0 है। यदि √ay(1)=π32 है तो 'α' का मान है
View Solution∫ax/2√a−x−ax का मान है
View Solution
