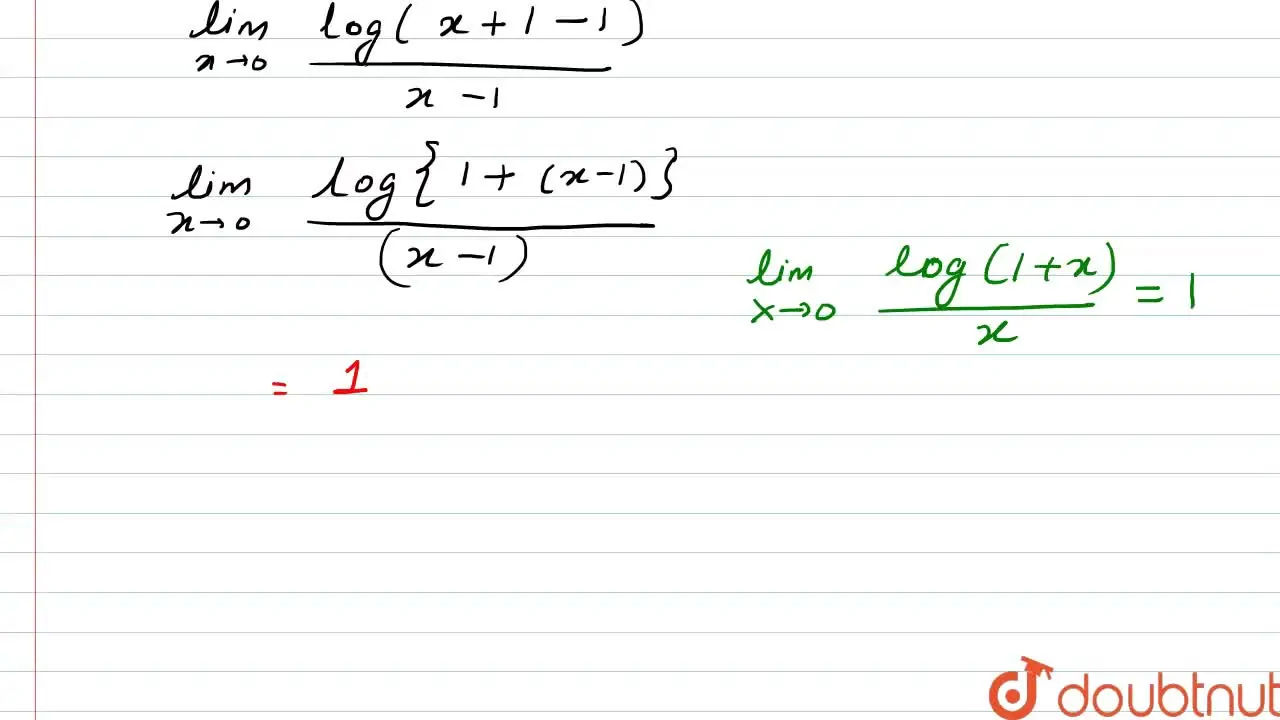Evaluate
Video Solution
Text Solution
The correct Answer is:
|
Updated on:21/07/2023
Related Playlists
- BOOK - NCERT ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - MISCELLANEOUS EXERCISE30videos
LIMITS AND DERIVATIVES
- BOOK - NCERT ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EXERCISE 13.211videos
LIMITS AND DERIVATIVES
- BOOK - NCERT ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EXERCISE 13.38videos
LIMITS AND DERIVATIVES
- BOOK - NCERT ENGLISHCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - EXERCISE 12.14videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
- BOOK - NCERT ENGLISHCHAPTER - LINEAR INEQUALITIESEXERCISE - EXERCISE 6.210videos
LINEAR INEQUALITIES
Similar Questions
Evaluate limx→∞logexx
View SolutionEvaluate (limx→∞)⎛⎜ ⎜⎝x(log)e⎧⎪ ⎪⎨⎪ ⎪⎩sin(a+1x)sina⎫⎪ ⎪⎬⎪ ⎪⎭⎞⎟ ⎟⎠, 0<a<π2
View SolutionEvaluate : (lim)x→1x2+x(log)ex−(log)ex−1(x2−1)
View SolutionEvaluate: limx→0e−(1+x)1xx
View SolutionEvaluate: limx→0log(1−3x)5x−1
View SolutionIf the graph of the function y=f(x) has a unique tangent at the point (a,0) through which the graph passes, then evaluate (lim)x→a(log)e{1+6f(x)}3f(x)
View SolutionEvaluate: limx→0log(ex−x)1−cosx
View SolutionEvaluate the following limit: (lim)x→0log(1+x)3x−1
View SolutionEvaluate: (lim)x→2x−2(log)a(x−1)
View SolutionEvaluate: (lim)x→0(1+x)cosecx
View Solution