Find the area of the shape shown in the figure 10.10.
This figure is made up of line-segments.
Moreover, it is covered by full squares and halfsquares only.
This makes our job simple.
(i)Fullyfilledsquares=3
(ii)Half-filled squares=3
Area covered by full squares=3×1 sq units<br>=3squnits
Totalarea=4(12) sq units
Related Playlists
- BOOK - NCERT ENGLISHCHAPTER - MENSURATIONEXERCISE - EXERCISE 10.21videos
MENSURATION
- BOOK - NCERT ENGLISHCHAPTER - MENSURATIONEXERCISE - EXERCISE 10.116videos
MENSURATION
- BOOK - NCERT ENGLISHCHAPTER - KNOWING OUR NUMBERSEXERCISE - EXERCISE 1.33videos
KNOWING OUR NUMBERS
- BOOK - NCERT ENGLISHCHAPTER - PLAYING WITH NUMBERSEXERCISE - EXERCISE 3.14videos
PLAYING WITH NUMBERS
Similar Questions
Find the area of the shaded field shown in figure.
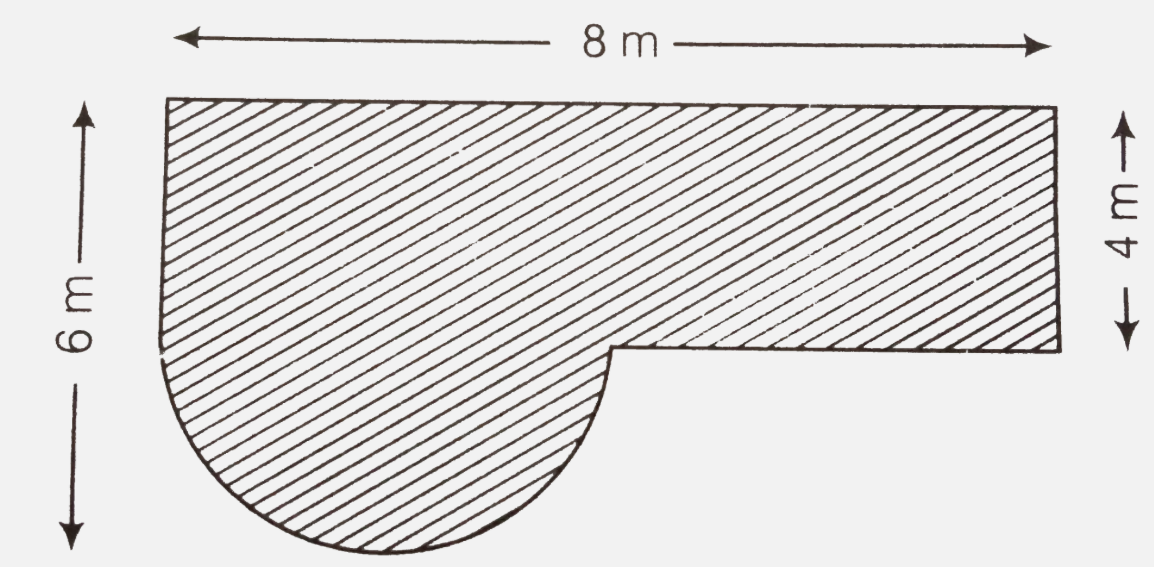 View Solution
View SolutionIn the figure, ABCD is a rectangle and E is a point on the side AB. If AB=10andAD=5 what is the area of the shaded region in the figure?
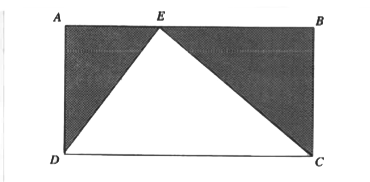 View Solution
View SolutionFind the magnetic induction at point O, if the current carrying wire is in the shape shown in the figure.
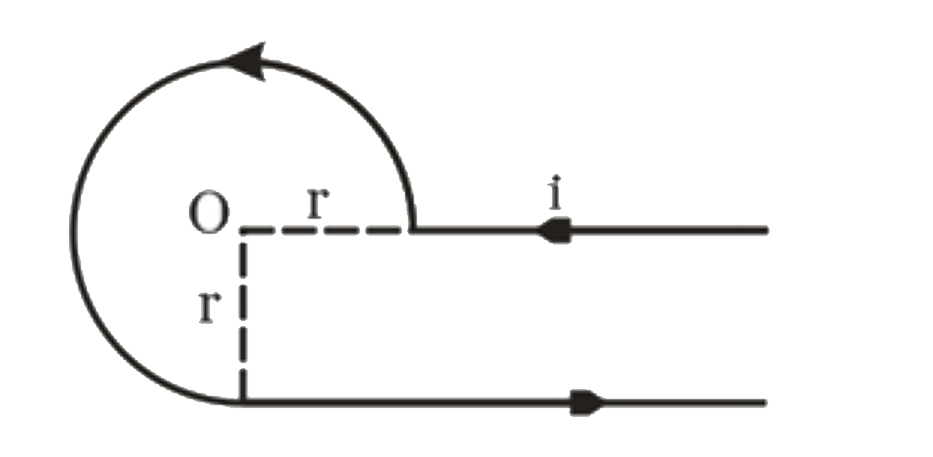 View Solution
View SolutionFind the area of the field shown in Figure by dividing it into a square, a rectangle and a trapezium.
View SolutionFind the area of the pentagonal park shown in Figure in two different ways:
View SolutionFind the acceleration of the two blocks shown in figure-2.101.Take g=10m/s2
View SolutionA very long straight conductor and an isosceles triangular conductor lie in a plane and are separated from each other as shown in the figure. If a = 10 cm, b = 20 cm, and h = 10 cm find the coefficient of mutual induction.
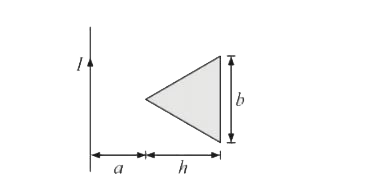 View Solution
View SolutionA very long straight conductor and an isosceles triangular conductor lie in a plane and are separated from each other as shown in the figure. If a = 10 cm, b = 20 cm, and h = 10 cm find the coefficient of mutual induction.
 View Solution
View SolutionA very long conductor and an isosceles triangular conductor lie in a plane and are separated from each other as shown in the figure. Find the coefficient of mutual induction. (a = 10 cm, b = 20 cm, h = 10 cm)
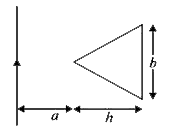 View Solution
View Solution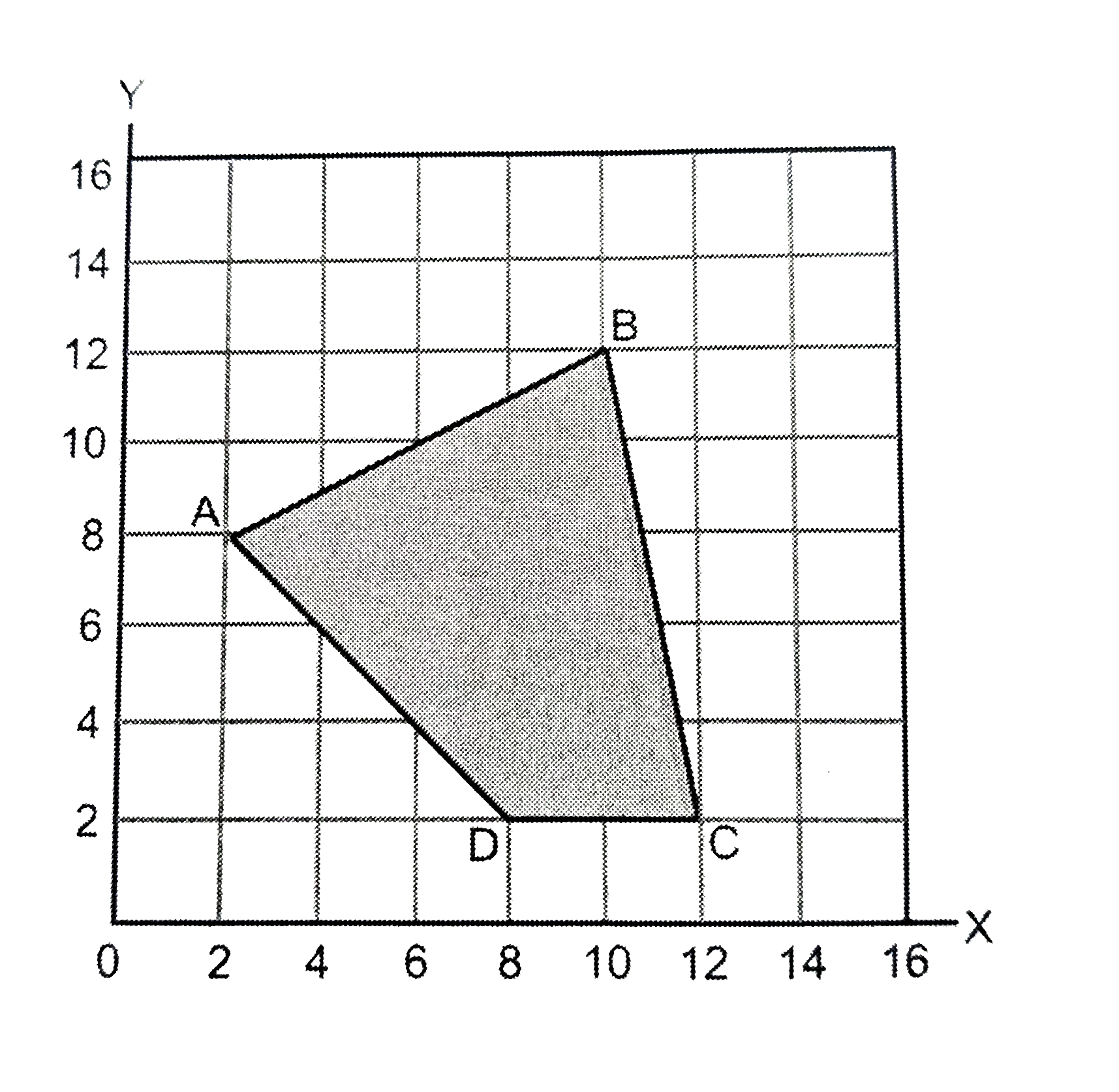
What is the area of the quadrilateral ABCD as shown in the figure above?View Solution


