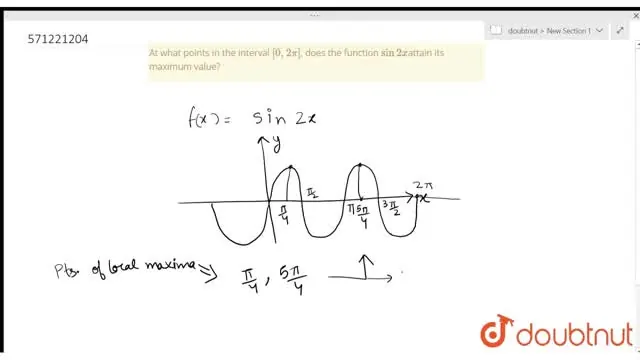
At what points in the interval [0,2π], does the function sin2x attain its maximum value?
Maximun value of function sin(2x) is 1 and that happens when
x=(2n+1)π2 {Where n is (0,1,2,..........)}
so number of places where sin(2x) will attain maxima in the given domain will be at
x=π2,3π2
i.e., for n=0 and 1
Related Playlists
- BOOK - NCERT ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - EXERCISE 6.118videos
APPLICATION OF DERIVATIVES
- BOOK - NCERT ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - EXERCISE 6.219videos
APPLICATION OF DERIVATIVES
- BOOK - NCERT ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - EXERCISE 6.49videos
APPLICATION OF DERIVATIVES
- BOOK - NCERT ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - EXERCISE 8.27videos
APPLICATION OF INTEGRALS
Similar Questions
In the interval (0,π/2) the fucntion f(x)=tannx+cotnx attains
View SolutionFind values of x on the interval [0,π] for which cosx≤sin2x.
View SolutionThe point in the interval (0,2π) where f(x)=exsinx has maximum slope is
View SolutionIn the interval [0,1], the function x25(1−x)75 takes its maximum value at the point (a) 0 (b) 14 (c) 12 (d) 13
View SolutionNumber of stationary points in [0,π] for the function f(x)=sinx+tanx−2x is:
View SolutionThe function S(x)=∫x0sin(πt22)dt has two critical points in the interval [1,2.4]. One of the critical points is a local minimum and the other is a local maximum .
The local maximum occurs at x equals _____View SolutionIt is given that at x=1 , the function x4−62x2+ax+9 attains its maximum value on the interval [0, 2] . Find the value of a .
View SolutionThe number of values of x in the interval [0,3π] satisfying the equation 2sin2x+5sinx−3=0 is
View SolutionThe number of values of x where the function f(x)=cosx+cos(√2x) attains its maximum value is
View SolutionFind the values of x in the interval [0,2π] for which 4sin2x−8sinx+3≤0
View Solution