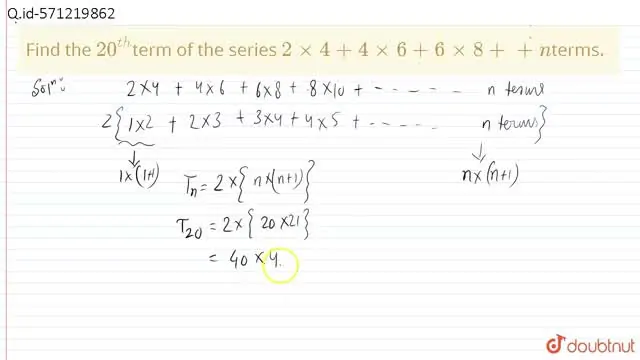Find the 20thterm of the series 2×4+4×6+6×8+...+nterms.
Video Solution
Text Solution
The given series is 2 × 4+4 × 6+ 6 × 8+....+n terms
n term=an
=2n×(2n+2)
=4n2+4n
a20 =4(20)2
+4(20)
=1600+80
=1680
Thus, the 20th term of the series is 1680.
|
Updated on:21/07/2023
Related Playlists
- BOOK - NCERT ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - SOLVED EXAMPLES24videos
SEQUENCES AND SERIES
- BOOK - NCERT ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - EXERCISE 9.218videos
SEQUENCES AND SERIES
- BOOK - NCERT ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2.35videos
RELATIONS AND FUNCTIONS
- BOOK - NCERT ENGLISHCHAPTER - SETSEXERCISE - EXERCISE 1.57videos
SETS
Similar Questions
Find the sum to n terms of the series :3×12+5×22+7×32+...
View SolutionFind the sum of the series
3×5+5×7+7×9+.. to n termsView SolutionFind the 20th term and the sum of 20 terms of the series: 2×4+4×6+6×8+..........
View SolutionFind the sum to n terms of the series :52+62+72+...+202
View SolutionFind the sum to n terms of the series :52+62+72+...+202
View SolutionFind the 20thand nthterms of the G.P. 52,54,58,...
View SolutionFind the nth term of the series :
1,2,4,8,.........View SolutionFind the sum to n terms of the series 1×2+2×3+3×4+4×5+......
View SolutionFind the sum to n terms of the series 1×2+2×3+3×4+4×5+......
View SolutionFind the sum to n terms of the series :1×2×3+2×3×4+3×4×5+...
View Solution