Question

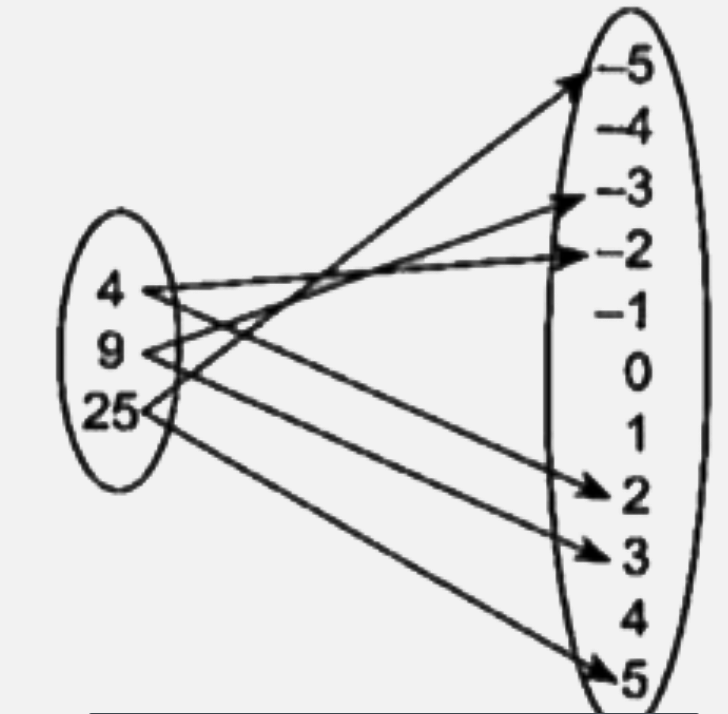
The Figure shows a relationship between the sets P and Q. Write this relation(i) in set-builder form (ii) roster form.What is its domain and range?

Options

A. if p`p/r` and cos R.`p/q`

Explanation

To solve the problem step by step, we will first define the relationship between the sets P and Q, then express it in set-builder and roster forms, and finally determine the domain and range.

Step 1: Define the Relationship
From the video transcript, we can see that the relationship between the sets P and Q is defined by the equation:
\( P = Q + 2 \)

Step 2: Identify the Elements of Sets P and Q
According to the transcript:
- Set P consists of the integers from 5 to 7.
- Set Q consists of the integers from 3 to 5.

Step 3: Write the Relation in Set-Builder Form
In set-builder notation, we can express the relation R as:
\( R = \{ (P, Q) \mid P = Q + 2, \, P \in \{5, 6, 7\}, \, Q \in \{3, 4, 5\} \} \)

Step 4: Write the Relation in Roster Form
To express the relation in roster form, we will find the pairs (P, Q) that satisfy the relationship \( P = Q + 2 \):
- If \( Q = 3 \), then \( P = 3 + 2 = 5 \) → (5, 3)
- If \( Q = 4 \), then \( P = 4 + 2 = 6 \) → (6, 4)
- If \( Q = 5 \), then \( P = 5 + 2 = 7 \) → (7, 5)

Thus, the relation in roster form is:
\( R = \{ (5, 3), (6, 4), (7, 5) \} \)

Step 5: Determine the Domain and Range
- Domain: The domain consists of all the first elements of the ordered pairs in the relation R. From the pairs (5, 3), (6, 4), and (7, 5), the domain is:
\( \text{Domain} = \{5, 6, 7\} \)

- Range: The range consists of all the second elements of the ordered pairs in the relation R. From the pairs (5, 3), (6, 4), and (7, 5), the range is:
\( \text{Range} = \{3, 4, 5\} \)

Final Summary
1. Set-Builder Form:
\( R = \{ (P, Q) \mid P = Q + 2, \, P \in \{5, 6, 7\}, \, Q \in \{3, 4, 5\} \} \)

2. Roster Form:
\( R = \{ (5, 3), (6, 4), (7, 5) \} \)

3. Domain:
\( \{5, 6, 7\} \)

4. Range:
\( \{3, 4, 5\} \)