(a) Using the necessary ray diagram, derive the mirror formula for a concave mirror.
(b) In the magnified image of a measuring scale (with equidistant markings) lying along the principal axis of a concave mirror, the markings are not equidistant. Explain.
The correct Answer is:a
(a) Figure, shows ray diagram explaining formation of a real image of a linear object AB placed in front of a concave mirror MPN of focal length f Since aperture of mirror is small, hence MP be considered to be a straight line.
Let us consider right angled triangles A.B.F and MPF, which are similar triangles. Therefore,
But as PM= AB, hence, we have
....(i)
Again triangles APB and A.PB. are also similar triangles and we have
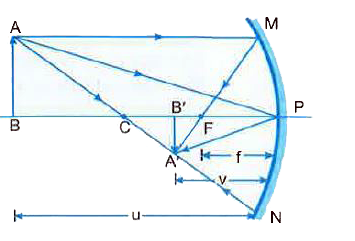
Comparing (i) and (ii), we get
As per sign convention followed: BP = -u, B.P =-v, and FP =-f Therefore, we get
or
Dividing throughout by uvf, we get
, which is the requisite mirror formula.
(b) Magnification of a mirror is given as:
As different markings of a measuring scale lying along the principal axis of a concave mirror are at different positions (i.e., u is different for them), we get magnified images of these marks but magnification differs from one mark to another. As a result, the markings in image are not equidistant.
Related Playlists
- BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D6videos
EXAMINATION PAPER 2020 (SOLVED)
- BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION B9videos
EXAMINATION PAPER 2020 (SOLVED)
- BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SELF ASSESSMENT TEST1videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - U-LIKE SERIESCHAPTER - MAGNETISM AND MATTEREXERCISE - SELF ASSESSMENT TEST (Section D)1videos
MAGNETISM AND MATTER
Similar Questions
(a) With the help of a suitable ray diagram, derive the mirror formula for a concave mirror.
View SolutionWith the help of a suitable ray diagram, derive the mirror formula for a concave mirror.
View SolutionRay diagram for Concave Mirror
View SolutionIs the virtual image formed by a concave mirror always magnified ?
View SolutionDraw ray diagram to shown the principal focus of a (i) concave mirror, (ii) convex mirror.
View SolutionA ray of light moving along the principal axis is falling on a concave mirror. In which direction is it reflected ?
View SolutionDraw a ray diagram to show image formation when the concave mirror produces a real inverted and magnified image of the object
View SolutionDraw a concave mirror and a convex mirror and mark the reflecting surfaces on both.
View SolutionDraw ray diagrams showing the image formation by a concave mirror when an object is placed at centre of curvature of the mirror
View SolutionWhen a ray of light travelling parallel to the principal axis of a concave mirror strikes at the polished surface of mirror, the reflected ray
View Solution

