The displacement of two interfering light waves are y1=4sinωt and y2=3cosωt. The amplitude of the resultant wave is (y1 and y2 are in CGS system)Solution in Telugu
5 cm
7 cm
1 cm
zero
The correct Answer is:A
Step by step video, text & image solution for The displacement of two interfering light waves are y_(1) = 4 sin omega t and y_(2) = 3 cos omega t. The amplitude of the resultant wave is (y_(1) and y_(2) are in CGS system) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - Practice Sheet (Exercise - I) (INTERFERENCE & YDSE) (Level - II (Advanced) Straight Objective Type questions9videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - Practice Sheet (Exercise - I) (INTERFERENCE & YDSE) (Level - II (Advanced) More than one correct answer type questions2videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET Exercise - III POLARLISATION (Level-II (Straight objective Type questions))8videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)81videos
WAVE MOTION AND SOUND
- BOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)15videos
WAVES
Similar Questions
A beam of light consisting of two wavelength , 6500A∘ and 5200A∘ is used to obtain interference fringes in a Young's double slit experiment (1Å=10−10m). The distance between the slits 2.0 mm and the distance between the plane of the slits and the screen is 120 cm. Find the distance of the third bright fringe on the screen from the central maximum for the wavelength 6500Å.
04:38View SolutionThe figure shows two points source which emit light of wavelength λ in phase with each other and are at a distance d=5.5λ apart along a line which is perpendicular to a large screen at a distance L from the centre of the source. Assume that d is much less than L. Which of the following statement is (are) correct ?
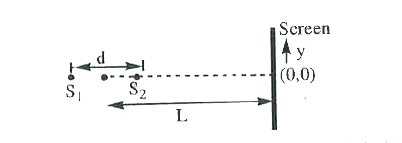 03:10View Solution
03:10View SolutionUnpolarised light of intensity 32Wm−2 passes through three polarisers such that the transmission axis of the last polariser is crossed with first. If the intensity of the emerging light is 3Wm−2, the angle between the axes of the first two polarisers is
02:39View SolutionA wave is described by the equation
y=(1.0mm)sinπ(x2.0cm−10.01s)
Find the time period and the wavelength.02:43View SolutionWhen a train is approaching the stationary observer, the apparent frequency of the whistle observed as 100 Hz, while when it has passed away from the observer with same speed, it is 50 Hz. Calculate the frequency of the whistle when the observer moves with the train (V = 330 m/s)
03:44View SolutionTwo light waves are represented by y_(1)=a sin_(omega)t and y_(2)= a sin(omega t+delta) . The phase of the resultant wave is
04:34View SolutionThe displacements of two intering lightwaves are y_(1) = 4 sin omega t and y_(2) = 3 cos(omega t) . The amplitude of the resultant wave is ( y_(1) and y_(2) are in CGS system)
02:29View SolutionThe displacements of two interfering light waves are y_(1) = 2sin omega t and y_(2) = 5sin (omega t+(pi)/(3)) the resultant amptitude is
03:07View SolutionTwo wave are represented by equation y_(1) = a sin omega t and y_(2) = a cos omega t the first wave :-
01:45View SolutionTwo waves are represented by y_(1)= a sin (omega t + ( pi)/(6)) and y_(2) = a cos omega t . What will be their resultant amplitude
02:50View SolutionThe equations for displacement of two light waves forming interference pattern are y_(1) = 4 sin omega t and y_(2) =3 sin (omega t+ (pi)/(2)) . Determine the amplitude of the resultant wave.
View SolutionEquations of two light waves are y1= 4 sin ω t and y2=3sin(ωt+π2). What is the amplitude of the resultant wave as they superpose on each other?
07:36View SolutionThe displacement of two interfering light waves are given by y1=3sinωt,y2=4sin(ωt+π/2). The amplitude of the resultant wave is
View Solutiony1=asinωt और y2=bcosωt द्वारा निरूपित दो तरंगों में कलान्तर है :
03:00View SolutionWhen the waves y_(1) = A sin omega t and y_(2) = A cos omega t are superposed, then resultant amplitude will be
02:43View Solution
