A projective of 2kg was velocities 3mls and 4mls at two points during its flight in the uniform gravitational field of the earth. If these two velocities are ⊥ to each other then the minimum KE of the particle during its flight isSolution in Telugu
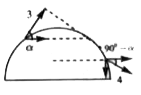
V1cosα=V2cos(90−α)
3cosα=4sinα
tanα=34
KEman=12mv21cos2α
12×2×3×(45)2=9×1625=5.76 J
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - SHORT ANSWER TYPE QUESTIONS6videos
MOTION IN A PLANE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS10videos
MOTION IN A PLANE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)7videos
MOTION IN A PLANE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
Similar Questions
Show that the trajectory of an object thrown at certain angle with the horizontal is a parabola .
04:33View SolutionWhat is the acceleration of a projectile at the top of its trajectory ?
06:08View SolutionA particle ‘P is moving in a circle of radius "r" with uniform speed v. AB is the diameter of circle and 'C' is the centre. The angular velocity of P about A and C are in the ratio.
04:44View SolutionGive two examples of the motion of big objects where the object can be treated as a particle and where it cannot be?
10:01View SolutionA projectile of 2kg has velocities 3m/s and 4m/s at two points during its flight in the uniform gravitational field of the earth. If these two velocities are ⊥ to each other then the minimum KE of the particle during its flight is
View SolutionA projectile of mass 2kg has velocities 3m//s and 4m/s at two points during its flight in the uniform gravitational field of the earth. If these two velocities are perpendicular to each other, then the minimum kinetic enerty of the particle during its flight is
02:56View SolutionThe distance travelled by a body during last second of its total flight is d when the body is projected vertically up with certain velocity. If the velocity of projection is doubled, the distance travelled by the body during last second of its total flight is (A) 2d (B) d (C) 2d + g/2 (D) 2d –g/2
View SolutionStatement I: During the flight of a projectile, the horizontal component of its velocity remains uniform .
Statement II: The vertical component of the velocity of a projectile becomes zero at the highest point of its path.View SolutionA fly ball is hit to the outfield. During its flight (ignore the effects of the air), what happens to its (a) horizontal and (b) vertical components of velocity? What are the (c ) horizontal and (d) vertical components of its acceleration during ascent, during descent, and at the topmost point of its flight?
View Solutionएक समान चुंबकीय क्षेत्र की दिशा के अनुदिश एक आवेशित कण प्रक्षेपित किया जाता है। तब इसका वेग
04:52View SolutionThe distance travelled by a body during last second of its total flight is d when the body is projected vertically up with certain velocity. If the velocity of projection is doubled, the distance travelled by the body during last second of its total flight is
View SolutionA projective of 2kg was velocities 3mn/ sand 4m/s of two points during its flight in the uniform gravitational field of the earth. If these two velocities are ⊥ to each other then the minimum KE of the particle during its flight is
View SolutionThe distance travelled by a body during last second of its total flight is d when the body is projected vertically up with certain velocity.If the velocity of projection is doubled ,the distance travelled by the body during last second of its total flight is
View SolutionThe distance travelled by a body during last second of its upward journey is d when the body is projected with certain velocity vertically up. If the velocity of projection is doubled, the distance travelled by the body during last second of its upward journey is
05:41View SolutionA projectile of 2kg was velocities 3m/s and 4m/s at two points during its flight in the uniform gravitational field of the earth. If these two velocities are ⊥ to each other then the minimum KE of the particle during its flight is
View Solution
