The points P, Q, R, S, T, U, A and B on the number line are such that, TR = RS = SU and AP = PQ = QB. Name the rational numbers represented by P, Q, R and S.
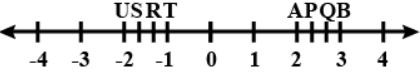
We are given, TR=RS=SU
T=−1=−1∗31∗3=−33
U=−2=−2∗31∗3=−63
So, numbers between T and U will be −43 and −53.
As, R is closer to T than S.So,
R=−43
S=−53
Also, we are given,
AP=PQ=QB
A=2=2∗31∗3=63
B=3=3∗31∗3=93
So, numbers between A and B will be 73 and 83.
As, P is closer to A than Q.So,
P=73
Q=83
Topper's Solved these Questions
- RATIONAL NUMBERSBOOK - NCERTCHAPTER - RATIONAL NUMBERSEXERCISE - EXERCISE 9.2
4 Videos
- RATIONAL NUMBERSBOOK - NCERTCHAPTER - RATIONAL NUMBERSEXERCISE - SOLVED EXAMPLES
6 Videos
- PERIMETER AND AREABOOK - NCERTCHAPTER - PERIMETER AND AREAEXERCISE - EXERCISE 11.2
8 Videos
- SIMPLE EQUATIONSBOOK - NCERTCHAPTER - SIMPLE EQUATIONSEXERCISE - EXERCISE 4.3
3 Videos
Similar Questions
Let O, P and Z represent the numbers 0, 3 and -5 respectively on the number line. Points Q, R and S are between O and P such that OQ = QR = RS = SP.
What are the rational numbers represented by the points Q, R and S. Next choose a point T between Z and O so that ZT = TO. Which rational number does T represent?
View SolutionFind the vlaues of P,Q,R,S and T on the given number line.

View Solution
Knowledge Check
P and Q are points on the line joining A(-2,5) and B(3,1) such that AP=PQ=QB. Then the mid pont of PQ is
A(12,3)B(−12,4)C(2,3)D(1,4)If pq and rs are two rational numbers then the relation ∣∣∣pq∣∣∣<∣∣rs∣∣ is :
AA. always trueBB. always falseCC. never trueDD. none of theseP and Q are points on the line joining A(-2,5) and B(3,1) such that AP=PQ=QB. Then the mid pont of PQ is
A(12,3)B(−12,4)C(2,3)D(1,4)
PQRSTU is a regular hexagon. Determine each angle of PQT .
View SolutionIn Fig. 4.238, S and T are points on the sides PQ and PR respectively of PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of PST and PQR . (FIGURE)
View SolutionIf P and Q are two points on the line joining A(-2,5),B(3,1) such that AP=PQ=QB then PB=
View SolutionThe coordinates of the points A and B are, respectively, (-3, 2) and (2, 3). P and Q are points on the line joining A and B such that AP = PQ = QB. A square PQRS is constructed on PQ as one side, the coordinates of R can be
View SolutionIf p,q,r and s are positive real numbers such that p+q+r+s=2, then M=(p+q)(r+s) satisfies the relation, when (A) 0<M≤1 (B) 1≤M≤2 .(C) 2≤M≤3 (D) 3≤M≤4
View Solution
