Two resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series , (b) in parrallel. Find the equivalent resistance of the (a) series combination , (b) parallel combination . Use for (a) the relation R=R1+R2and for (b) 1R=1R1+1R2andΔR'R,2=ΔR1R21+ΔR2R22 Solution in Telugu
(a) The equivalent resistance of series combination
R=R1+R2=(100±3) ohm + (200±4) ohm = 300 ±7 ohm
(b) The equivalent resistance of parallel combination
R.=R1R2R1+R2=2003=66.7 ohm
Then, from 1R,=1R1+1R2
We get , ΔR.R,2=ΔR1R21+ΔR2R22
=(66.7100)23+(66.7200)24=1.8
Then , R.=66.7pm 1.8ohm(Here, DeltaR is expressed as 1.8 instead of 2 of keep in conformity with the rules of significant figures.
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBook:AAKASH SERIESChapter:UNITS AND MEASUREMENTSExercise:SHORT ANSWER TYPE QUESTIONS
Explore 16 Videos
- UNITS AND MEASUREMENTSBook:AAKASH SERIESChapter:UNITS AND MEASUREMENTSExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 24 Videos
- UNITS AND MEASUREMENTBook:AAKASH SERIESChapter:UNITS AND MEASUREMENTExercise:PRACTICE EXERCISE
Explore 45 Videos
- WAVE MOTIONBook:AAKASH SERIESChapter:WAVE MOTIONExercise:PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)
Explore 10 Videos
Similar Questions
How do the random errors differ from systmetic errors?
View SolutionBy taking precautions, can we minimize the random erros?
View SolutionThe ratio of S.I. unit of universal gravitational constant to C.G.S. unit is
View SolutionA source emitting sound of frequency 180 Hz is placed in front of a wall at a distance of 2m from it. a detector is also placed in front of the wall at the same distance from it. The minimum distance between the source and the detector is x mtrs for which the detector shows a maxima of sound. Speed of sound in air = 360 m/s
View SolutionTwo resistances R_1 and R_2 are made of different materials. The temperature coefficient of the material of R_1 is alpha and of the material of R_2 is -beta . The resistance of the series combination of R_1 and R_2 will not change with temperature, if R_1//R_2 equals.
View SolutionFor two resistors R_1 and R_2 , connected in parallel, find the relative error in their equivalent resistance. if R_1=(50 pm2)Omega and R_2=(100 pm 3) Omega .
View SolutionProve it R= R_1 + R_2 Where R is the resistors connected in series R_1 And R_2 Is the equivalent resistance of. (b) Prove: 1/R = 1/(R_1) + 1/(R_2) Where R is the resistors connected in the sequence R_1 And R_2 Is the equivalent resistance of.
View SolutionThe magnitudes of the gravitational fields at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M are F1 and F2 respectively then
(a)F1F2=r1r2 if r1<R and r2<R
(b)F1F2=(r2r1)2 if r1>R and r2>R
(c)F1F2=r1r2 if r1>R and r2>R
(d)F1F2=(r1r2)2 if r1<R and r2<R
View SolutionThe combined resistance R of two resistance R1andR2, where R1,R2≥0 is given by (1R)=(1R1)+(1R2). If R1+R2=c (where c is constant), show that the maximum resistance R is obtained by choosing R1=R2
View SolutionTwo resistances r1 and r2(r1<r2) are joined in parallel. The equivalent resistance R is such that
View SolutionFor two resistors R1 and R2, connected in parallel, find the relative error in their equivalent resistance. if R1=(50±2)Ω and R2=(100±3)Ω.
View Solutionযদি rr1+log(r2r1)=1 এবং r2=er হয়, তবে দেখাও যে, r1rlog(r1r)=1
View SolutionThe combined resistance R of two resistors R_1 and R_2(R_1,R_2>0) is given by 1/R=1/R_1+1/R_2 . If R_1+R_2=C (a constant), show that the maximum resistance R is obtained by choosing R_1=R_2 .
View Solutionଦୁଇଟି ପ୍ରତିରୋଧ R1 ଓ R2 ମଧ୍ୟରୁ R1>R2 |ସେମାଙ୍କୁ ସମାନ୍ତର ସଂଯୋଗ କଲେ ଯଦି ସମତୁଲ୍ୟ ପ୍ରତିରୋଧ R ହେଲା ତେବେ R, R1ଓR2 ମଧ୍ୟରେ ସମ୍ପର୍କଟି କ'ଣ ହେବ ?
View SolutionOhms law experiment is performed seperately with individual resistors R1,R2(R1>R2) and series combination of R1,R2Graph us placed between potential difference V and current I as shown in figure for each case.Identify which one is for R1,R2 and combination of resistors?in the graph A,B,C respectively represents
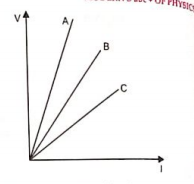
View SolutionWhen two resistors of resistance R1 and R2 are connected in parallel, the net resistance is 3 ohm. When connected in series. Its values of 16 ohm. Calculate the value of R1 and R2.
View Solution

