The area bounded by y=x+1andy=cosx and the x - axis, is
1 sq. units
32 sq. units
14 sq. units
18 sq. units
The correct Answer is:B
To find the area bounded by the curves y=x+1, y=cosx, and the x-axis, we will follow these steps:
Step 1: Identify the points of intersection
We need to find the points where the curves y=x+1 and y=cosx intersect. To do this, we set them equal to each other:
x+1=cosx
This equation cannot be solved algebraically, so we will find the points of intersection graphically or numerically.
Step 2: Graph the functions
We can sketch the graphs of y=x+1 and y=cosx to identify the points of intersection. The graph of y=cosx oscillates between -1 and 1, while the line y=x+1 is a straight line with a slope of 1.
From the graph, we can observe that the curves intersect at approximately x=−1 and x=0.
Step 3: Set up the integral for the area
The area A between the curves from x=−1 to x=0 can be calculated using the integral:
A=∫0−1(cosx−(x+1))dx
Step 4: Simplify the integrand
We simplify the integrand:
cosx−(x+1)=cosx−x−1
Step 5: Evaluate the integral
Now we will compute the integral:
A=∫0−1(cosx−x−1)dx
This can be split into three separate integrals:
A=∫0−1cosxdx−∫0−1xdx−∫0−11dx
Calculating each integral separately:
1. Integral of cosx:
∫cosxdx=sinxso(sinx)0−1=sin(0)−sin(−1)=0−(−sin(1))=sin(1)
2. Integral of x:
∫xdx=x22so(x22)0−1=0−(−1)22=−12
3. Integral of 1:
∫1dx=xso(x)0−1=0−(−1)=1
Putting it all together:
A=sin(1)−(−12)−1
A=sin(1)+12−1=sin(1)−12
Final Step: Calculate the area
Thus, the area bounded by the curves and the x-axis is:
A=sin(1)−12
We need to find the points where the curves y=x+1 and y=cosx intersect. To do this, we set them equal to each other:
We can sketch the graphs of y=x+1 and y=cosx to identify the points of intersection. The graph of y=cosx oscillates between -1 and 1, while the line y=x+1 is a straight line with a slope of 1.
The area A between the curves from x=−1 to x=0 can be calculated using the integral:
We simplify the integrand:
Now we will compute the integral:
∫cosxdx=sinxso(sinx)0−1=sin(0)−sin(−1)=0−(−sin(1))=sin(1)
∫xdx=x22so(x22)0−1=0−(−1)22=−12
∫1dx=xso(x)0−1=0−(−1)=1
A=sin(1)+12−1=sin(1)−12
Thus, the area bounded by the curves and the x-axis is:
Topper's Solved these Questions
- APPLICATION OF INTEGRALSBook:MTG-WBJEEChapter:APPLICATION OF INTEGRALSExercise:WE JEE PREVIOUS YEARS QUESTIONS (CATEGORY 2 : SINGLE OPTION CORRECT TYPE)
Explore 3 Videos
- APPLICATION OF DERIVATIVES Book:MTG-WBJEEChapter:APPLICATION OF DERIVATIVES Exercise:WB JEE Previous Years Questions ( CATEGORY 3 : One or More than One Option Correct Type (2 Marks) )
Explore 11 Videos
- BINOMIAL THEOREMBook:MTG-WBJEEChapter:BINOMIAL THEOREMExercise:WB JEE Previous Years Questions ( CATEGORY 1 : Single Option Correct Type (1 Mark))
Explore 13 Videos
Similar Questions
Knowledge Check
If A1 is the area bounded by the curve y = cos x and A2 is the area bounded by y = cos 2 x along with x - axis from x = 0 and x=π0, then
AA1=√32,A2=√34BA1=√32,A2=12CA1A2=21DA1A2=√31The area bounded by y=−x2+1 and the x-axis is
A13B23C43D83The area bounded by y=max(x2,x4),y=1 and the y - axis from x=0 to x=1 is
A3 sq. unitsB32 sq. unitsC23 sq. unitsD12 sq. units
The area bounded by y=x2,y=[x+1],x≤1 and the y axis is
View SolutionCompute the area of the figure bounded by the lines y=x+1,y=cosx and the x-axis
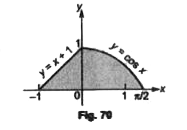
View SolutionThe area bounded by y=cosx,y=x+1,y=0 is
View SolutionThe area bounded by y=ex,Y - axis and the line y=e is
View SolutionThe area of the region bounded by the curve y=|x−2|,x=1,x=3 and the X-axis is
View Solution