Consider two coherent sources $S_{1} and S_{2}$ producing monochromatic waves to produce interference patten. Let the displacement of the wave produced by $S_{1}$ be given by
and the displacement by $S_{2} be Y_{1} = a cos ω t$
$Y_{2} = a cos (ω t - ϕ)$
Find out expression for the amplitude of the resultant displacement at a point and show that the intensity at that point will be
$I = 4 a^{2} {cos}^{2} ϕ / 2$
Hence establish the conditions for constructive and destructive interference.
(b) What is the effect on the interference friinges in Young's double slit experiment when (i) the width of the source slit is increased, (ii) the monochromatic source is replaced by a source is replaced by a source of white light ?
OR
(a) A ray, 'PQ' of light on the face AB of glass prism ABC (as shown in the figure) and emerges out of the face AC. Trace the path of the ray. Show that
$∠ i + ∠ e = ∠ A + ∠ δ$
Where $δ$ and e denote the angle of deviation and angle of emergence respectively.

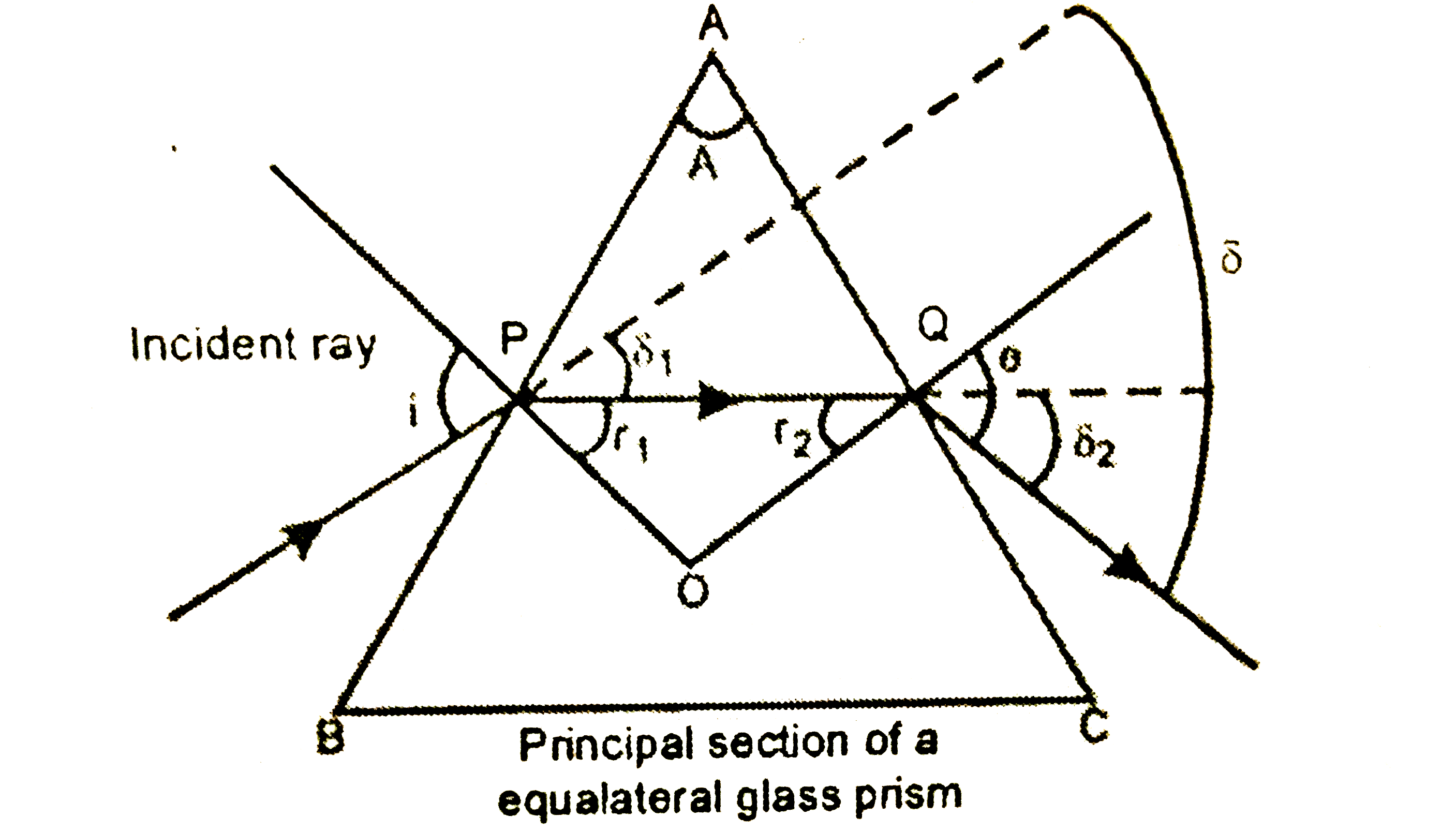
Plot a graph showing the variation of the angle of deviation as a function of angle of incidence. state the condition under which $∠ δ$ is minimum.
(b) Find out the relation between the refractive index $(μ)$ of the glass prism and $∠ A$ for the case when the angle of prism (A) is equal to the angle of minimum deviation $(δ_{m})$ . Hence obtain the value of the refractive index for angle $A e = 60^{\circ}$ .

Video Solution

Text Solution

Verified by Experts

(a) $S_{1} P = S_{2} P$
The distances $S_{1} P and S_{2} P$ are equal, waves from $S_{1} and S_{2}$ will take the same to travel to the point.
Displacement produced by the sources $S_{1}$ at the point P is given by
$y_{1} = a cos ω t$
The displacement produced by the sources $S_{2}$ (at point P) will alos be gibven by
$y_{2} = a cos ω t$
Thus, the resultant of displacement at P would be given by
$y = y_{1} + y_{2} = 2 a cos ω t$
The intensity is the poportional to the square of the amplitude, the resultant intensity will be given by
$I = 4 a^{2}$
$I_{o}$ represent the intensity produced by each of the individual sources.
$I_{o} α a^{2}$
In fact at any point on the prependicular bisector of $S_{1} S_{2}$ , the intensity will be $4 I_{o}$ as construct9ive interfernce next point is Q.
$S_{2} Q - S_{1} Q = 2 λ$
$y_{1} = a cos ω t$
if ,
the displacement produced by $S_{2}$ will be given by
$y_{2} = a cos (ω t - 4 π) = a cos ω t$
Next consdier point R :
$S_{2} R - S_{1} R = 2.5 λ$
$y_{1}, = a cos ω t$
$y_{2} = a cos ω t - 5 λ$
$= - a cos ω t$
A destructive interference andt eh resultant intensirt will be zero. so other arbitrary point $C_{1}$ .
The displacement produced by $S_{1}$ is given by
$y_{1} = n cos ω t$
$y_{2} = a cos (ω t + ϕ)$
and resultant displacement willl be given by
$y = y_{1} + y_{2}$
$a [cos ω t + cos (ω t + ϕ)]$
$2 a cos (\frac{ϕ}{2}) cos (ω t + \frac{ϕ}{2})$
The amplitude of the resultant displacement is $2 a cos (\frac{ϕ}{2})$ and therefore the intensity at that point will be
$I = 4 I_{o} {cos}^{2} (\frac{ϕ}{2})$
$if ϕ = 0 \pm 2 π, \pm 4 π$ ...., which correspoinds to the condition in costructive interference. Leading to maximum intensity, on the other hand, if
$ϕ = \pm π, \pm 3 π, 5 π$
which corresponds to the condition have destructive interference leading to zero intensity,
(b) (i) As the width of the slits ix increased, the fringe width decrease. It is beacause,
$β α \frac{1}{d}$
(ii) The different colours of white light will produce different interence patterns but the central bright friges due to all colours are at teh sme positions, therefore, the central bright fringe is white in colour. since the wavelength of the light is smallest, the fringe closest, on the either side of the central with frige is blue and fasthest is red. Beyond a few fringres, no clear patten is visible.
OR
(a) Let the incident ray meet refracting face AB of the prism at point P. Ray PQ is the refracted ray inside th prism and $δ_{2} and r_{1}$ are the angle of deviation and refraction at interface AB. At interface AC the ray goes out of the prism. Let e be the angle of emergence. The angle of deviation at point Q is $δ_{2}$ as shown in figure.

Using geometry, we see that at point P,
$i = δ_{1} + r_{1} δ_{1} = i - r_{1}$
and at point Q, $e = δ_{2} + r_{2}$
$δ_{2} = e - r_{2}$
The total deviation $δ$ , suffered by the incident ray is equal to $δ_{1} + δ_{2}$
$δ = δ_{1} + δ_{2}$
${(i - r_{1})}_{1}^{2} + (e - r_{2}) = (i + e) - (r_{1} + r_{2})$
In quadrilatent POQA, the sum of all four angle is $360^{\circ}$
$P + O + Q + A = 360^{\circ}$
as P and Q both are right angles.
$P + Q = 180^{\circ}$
$O + A = 180^{\circ}$
In triangle POQ
$O + r_{1} + r_{2} = 180^{\circ}$
In triangle POQ ,
$O + r_{1} + r_{2} = 180^{\circ}$
comparing equations (ii) and (iii), we have
$A = r_{1} + r_{2}$
Subsituting this value in equation (i)
$δ = i + e - A$
$δ + A = i + e$
(b) A ray of light incident on face AB will just suffer internal reflection at the other face, AC , if it goes incident on the face AC at an angle equal to the critical angle for the crititcal angle for the material of the prism. If critical angle for the material fo prism is C.
$sin C = \frac{1}{μ} = \frac{1}{1.524} = 0.6562$
$C = 41^{\circ}$
Now , for a prism,
$r_{1} + r_{2} = A$
$r_{2} = C$ we have
$r_{1} + C = A or r_{1} = A - c$
Setting , the values of A and C, we obtain,
$r_{1} = 69^{\circ} - 41^{\circ} = 1 9^{\circ}$
At the face, AB : $\frac{sin i}{{sin r}_{1} =} μ or \frac{sin i}{{sin 19}^{\circ}} = 1.524$
$sin i = 1.524 \times {sin 19}^{\circ}$
$= 1.524 \times 0.3256 = 0.4962$
$i = {29.75}^{\circ}$

Updated on:21/07/2023

Two waves $y_{1} = 3 sin ω t c m and Y = 4 cos (ω t + \frac{π}{2})$ cm product the interference pattern. Then the amplitude of the resultant wave will be
A1 cm
B3 cm
C4 cm
D5 cm
it the two waves represented dy $y_{1} = 4 cos ω t$ and $y_{2} = 3 cos (ω t + π / 3)$ interfere at a point, then the amplitude of the resulting wave will be about
A7
B5
C6
D $3.5$
$x_{1} = A sin (ω t - 0.1 x)$ and $x_{2} = A sin (ω t - 0.1 x - \frac{ϕ}{2})$ Resultant amplitude of combined wave is
A $2 A \frac{cos (ϕ)}{4}$
B $A \sqrt{2 cos ϕ / 2}$
C $2 A \frac{ϕ}{2}$
D $A \sqrt{2 (1 + \frac{cos (ϕ)}{4})}$