A capacitor, made of two parallel plates each of plate area A and separation d, is being charged by an external ac socurce. Show that the displacement current inside the same as the current charging the capacitor.
To show that the displacement current inside a capacitor is the same as the current charging the capacitor, we can follow these steps:
Step 1: Understand the Circuit
We have a capacitor made of two parallel plates, each with an area A and separated by a distance d. The capacitor is connected to an alternating current (AC) source, which can be represented as E(t)=E0sin(ωt).
Step 2: Relate Charge to Voltage
The charge q on the capacitor is related to the voltage V across it by the equation:
q=CV
where C is the capacitance of the capacitor given by:
C=ϵ0Ad
Thus, the charge on the capacitor when connected to the AC source becomes:
q=CE0sin(ωt)
Step 3: Differentiate Charge to Find Current
The current I flowing into the capacitor is the rate of change of charge with respect to time:
I=dqdt
Differentiating q with respect to time gives:
I=ddt(CE0sin(ωt))=CE0ωcos(ωt)
This can be expressed as:
I=I0cos(ωt)
where I0=CE0ω is the peak current.
Step 4: Calculate Displacement Current
The displacement current Id can be defined using the changing electric field between the plates of the capacitor. The electric field E between the plates is given by:
E=qϵ0A
The electric flux ΦE through the area A is:
ΦE=E⋅A=qϵ0
The displacement current is defined as:
Id=ϵ0dΦEdt
Substituting for ΦE:
Id=ϵ0ddt(qϵ0)=dqdt=I
From our previous calculation, we have:
Id=CE0ωcos(ωt)=I0cos(ωt)
Step 5: Conclusion
Since both the displacement current Id and the charging current I are equal to I0cos(ωt), we conclude that:
Id=I
Thus, the displacement current inside the capacitor is indeed the same as the current charging the capacitor.
We have a capacitor made of two parallel plates, each with an area A and separated by a distance d. The capacitor is connected to an alternating current (AC) source, which can be represented as E(t)=E0sin(ωt).
The charge q on the capacitor is related to the voltage V across it by the equation:
q=CV
where C is the capacitance of the capacitor given by:
C=ϵ0Ad
Thus, the charge on the capacitor when connected to the AC source becomes:
q=CE0sin(ωt)
The current I flowing into the capacitor is the rate of change of charge with respect to time:
I=dqdt
Differentiating q with respect to time gives:
I=ddt(CE0sin(ωt))=CE0ωcos(ωt)
This can be expressed as:
I=I0cos(ωt)
where I0=CE0ω is the peak current.
The displacement current Id can be defined using the changing electric field between the plates of the capacitor. The electric field E between the plates is given by:
E=qϵ0A
The electric flux ΦE through the area A is:
ΦE=E⋅A=qϵ0
The displacement current is defined as:
Id=ϵ0dΦEdt
Substituting for ΦE:
Id=ϵ0ddt(qϵ0)=dqdt=I
From our previous calculation, we have:
Id=CE0ωcos(ωt)=I0cos(ωt)
Since both the displacement current Id and the charging current I are equal to I0cos(ωt), we conclude that:
Id=I
Thus, the displacement current inside the capacitor is indeed the same as the current charging the capacitor.
Topper's Solved these Questions
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:SET-II
Explore 35 Videos
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:SET-III
Explore 25 Videos
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:SET III
Explore 9 Videos
- SAMPLE PAPER 2019Book:XII BOARDS PREVIOUS YEARChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
A capacitor, made of two parallel plates each of plate are A and separation d, is being charged by an external a.c. source. Show that the displacement current inside the capacitor is the same as the current charging the capacitor.
View SolutionShow that displacement current is equal to conduction current during chargeing of a capacitor.
View Solution
Knowledge Check
A capacitor made of two circular plates each of radius 12 cm and separated by 5 mm. The capacitor is being charged by an external source. The charging current is constant and equal to 0.15 A. The capacitance of the parallel plate capacitor is
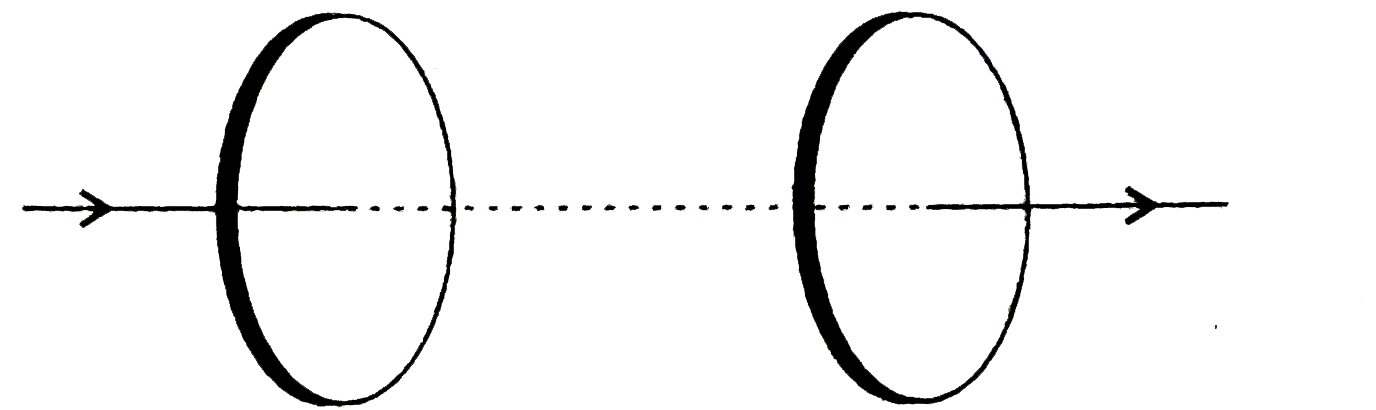 A40 pFB45 pFC70 pFD80 pF
A40 pFB45 pFC70 pFD80 pFIn a parallel-plate capacitor of plate area A, plate separation d and charge Q the force of attraction between the plates is F.
AF∝Q2BF∝1ACF∝dDF∝1d
A parallel capacitor is being charged by an external source. Show that the sum of conductor current and displacement current has the same value everywhere in the circuit.
View SolutionA parallel capacitor is being charged by an external source. Show that the sum of conductor current and displacement current has the same value everywhere in the circuit.
View SolutionA parallel plate capacitor made of two circular plates each of radius 10 cm and separated by 4.0mm. The capacitor is being charged by an external source. The charging current is constant and equal to 0.10A. Calculate (i) the capacitance (ii) the rate of change of potential difference between the plates (iii) the displacement current.
View SolutionFigure 8.01 shows a capacitor made of two circular plates each of radius 12 cm, and separated by 5.0 cm. The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15 A.
(a) Calculate the capacitance and the rate of charge of potential difference between the plates.
(b) Obtain the displacement current across the plates.
(c) Is Kirchhoff.s first rule (junction rule) valid at each plate of the capacitor? Explain.
View SolutionFig. shows a capacitor made of two circular plates each of radius 12 cm and separated by 5.0mm. The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15A.
(a) Calculate the capacitance and the rate of change of potential difference between the plates.
(b) Obtain the displacement current across the plates.
(c) Is Kirchhoff's first rule valid at each plate of the capacitor ? Explain.

View SolutionFigure shows a capacitor made of two circular plates each of radius 12cm, and separated by 5.0cm. the capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15A
(a) Calcuate the capacitance and the rate of change of potential difference between the plates
(b) Obtain the displacement current across the plates
(c) Is kirchhoff's first rule(junction rule) vaild at each plate of the capacitor ? Explain.
 .
.
View Solution
