Two point charges 4Q, Q are separated by 1m in air. At what point on the line joining the charges is the electric field intensity zero ?
Also calculate the electrostatic potential energy of the system of charges, taking the value of charge, Q=2×10−7C.
Step-by-Step Solution:
1. Identify the charges and their positions:
- Charge 4Q at position A
- Charge Q at position B
- Distance between A and B is 1m
2. Assume a point P on the line joining A and B where the electric field is zero:
- Let the distance from A to P be x
- Therefore, the distance from P to B is 1−x
3. Set up the equation for the electric field at point P:
- Electric field due to 4Q at P: E4Q=k⋅4Qx2
- Electric field due to Q at P: EQ=k⋅Q(1−x)2
4. Since the electric field at P is zero, the magnitudes of the fields must be equal:
k⋅4Qx2=k⋅Q(1−x)2
5. Simplify the equation:
4Qx2=Q(1−x)2
6. Cancel out common terms:
4x2=1(1−x)2
7. Take the square root of both sides:
2x=11−x
8. Solve for x:
2(1−x)=x
2−2x=x
2=3x
x=23
Part 2: Calculating the Electrostatic Potential Energy
1. Use the formula for electrostatic potential energy:
U=kQ1Q2r
2. Substitute the given values:
- Q1=4Q
- Q2=Q
- r=1m
- Q=2×10−7C
- k=9×109Nm2/C2
3. Calculate the potential energy:
U=9×109×(4×2×10−7)×(2×10−7)1
U=9×109×8×10−141
U=9×109×8×10−14
U=72×10−5
U=7.2×10−4J
- Charge 4Q at position A
- Charge Q at position B
- Distance between A and B is 1m
- Let the distance from A to P be x
- Therefore, the distance from P to B is 1−x
- Electric field due to 4Q at P: E4Q=k⋅4Qx2
- Electric field due to Q at P: EQ=k⋅Q(1−x)2
k⋅4Qx2=k⋅Q(1−x)2
4Qx2=Q(1−x)2
4x2=1(1−x)2
2x=11−x
2(1−x)=x
2−2x=x
2=3x
x=23
U=kQ1Q2r
- Q1=4Q
- Q2=Q
- r=1m
- Q=2×10−7C
- k=9×109Nm2/C2
U=9×109×(4×2×10−7)×(2×10−7)1
U=9×109×8×10−141
U=9×109×8×10−14
U=72×10−5
U=7.2×10−4J
Topper's Solved these Questions
Similar Questions
Two point charges of +3μC each are 100cm apart. At what point on the line joining the charges will the electric intensity be zero ?
View SolutionTwo point charges 4μCand−2μC are separated by a distance of 1m in air. Calculate at what point on the line joining the two charges is the electric potential zero ?
View Solution
Knowledge Check
Two point charges +4q and +q are placed 30cm apart. At what point on the line joining them is the electric field zero
A15 cm from charge qB20 cm from charge 4 qC7.5 cm from charge qD5cm from charge qTwo point charges Q and −Q/4 are separated by a distance X. Then
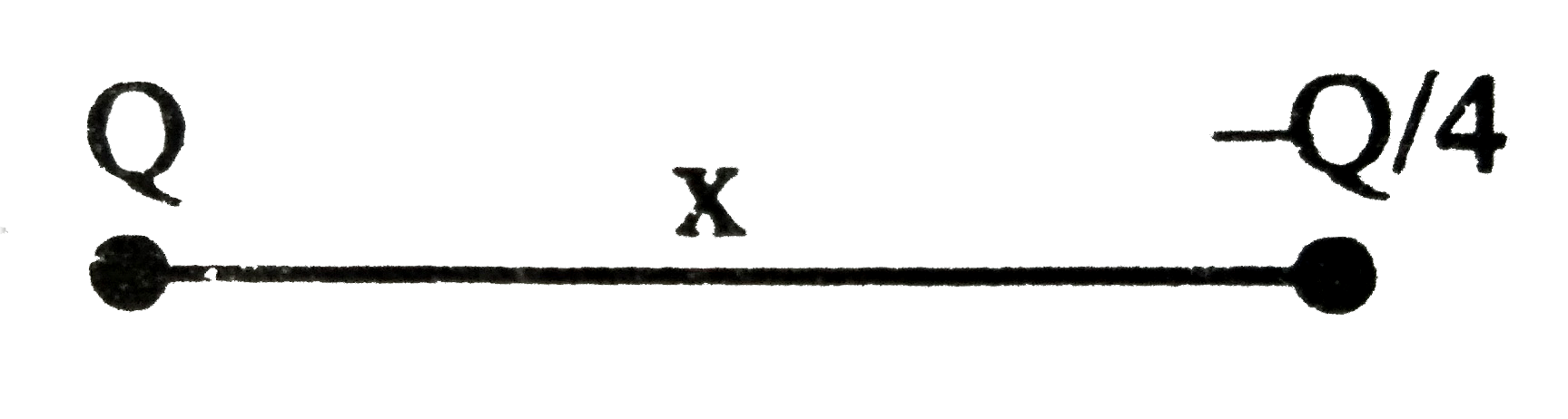 .Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.
.Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.The two point charges 4μC and 1μC are separated by a distance of 2 m in air. Find the point on the line joining the charges at which net electric field of the system is zero.
A43m from 1μCB23m from 1μCC43m from 4μCD23m from 4μC
Two point charges +4μCand−2μC are separated by a distance of 1 m in air. Calculate at what point on the line joining the two charges is the electric potential zero.
View SolutionTwo point charges 20×10−6Cand−4×10−6C are separated by a distance of 50cm in air, Find (i) the point on line joining the charges, where the electrostatic potential is zero (ii) Also, Calculate the electrostatic potential energy of the system.
View SolutionTwo point charges +4μCand+1μC are separated by a distance of 2 m in air. Find the point on the line joining the two charges at which the net electric field of the system is zero.
View SolutionTwo charges 3×10−8Cand−2×10−8C are located 15 cm apart. At what point on the line joining the two charges is the electric potential zero ? Take the potential at infinity to be zero.
View SolutionTwo charge _q and -3q are placed at a distance of 1 m apart.Find out the points on the line joing two charges, where electric potential is zero.
View Solution

