A ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take g=10ms−2. Solution in Gujrati
(a) Let us take the y-axis in the vertically upward direction with zero at the ground, as shown in Fig.
Now υ0=+20ms−1,
a=−g=−10ms−2,
υ=0ms−1
If the ball rises to height y from the point of launch, then using the equation
υ2=υ20+2(y−y0)
we get
0=(20)2+2(−10)(y−y0)
Solving, we get, (y−y0)=20m.
(b) We can solve this part of the problem in two ways.

Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NCERT GUJARATICHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISES
23 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT GUJARATICHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES
5 Videos
- MOTION IN A PLANEBOOK - NCERT GUJARATICHAPTER - MOTION IN A PLANEEXERCISE - EXCERCISES
30 Videos
- OSCILLATIONSBOOK - NCERT GUJARATICHAPTER - OSCILLATIONSEXERCISE - Additional Exercises
6 Videos
Similar Questions
The angle of elevation of a bird sitting on top of a tree as seen from the point at a distance of 20m from the base of the tree is 60∘. Then, the height of the tree is ……..m
View SolutionA boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can equal to 49 ms-1. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of 5 ms−1 and the boy again throws the ball up with the maximum speed he can, how long goes the ball take to return to his hands ?
View SolutionState , for each of the following physical quantities , if it is a scalar or a vector : volume , mass , speed , acceleration , density , number of moles , velocity , angular frequency , displacement , angular velocity .
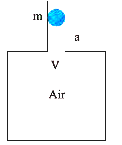
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
View SolutionA ball is thrown vertically upwards with a velcotiy of 20 ms^(-1) from the top of a multi-storey building. The height of the point fromwher the ball is thrown if 25-0m from the ground. (a) How high the ball will rise ? And (b) how long will it be before the ball hits the ground ? Take. g=10 ms^(-2) .
View SolutionA ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25 m from the ground. How long will it be before the ball hits the ground (Take, g=10ms−2) ?
View Solution25 मीटर ऊँचे मीनार से एक गेंद 10 मी/से के वेग से ऊर्ध्वाधर ऊपर की ओर फेंकी जाती है।
गेंद धरती से टकराने के पहले कितना समय लेगी ?
(g=10मी/से2)
View SolutionA ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multi-storey building. The height of the point from where the boll is thrown is 25.0m from the ground (a) How high will the ball rise? and (b) How long will it take to reach the ground?
View SolutionA ball is thrown vertically upwards with a velocity of 20ms^-1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. How high will the ball rise?
View SolutionA ball is thrown vertically upwards with a velocity of 20ms^-1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. How long will it be before the balls hits the ground? Take g=10ms^-2 [Actual value of g is 9.8ms^-2] .
View SolutionA ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take g=10ms−2.
View SolutionA ball is thrown vertically upwards with a velocity of 20 ms^(-1) from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take g = 10 ms^(-2) .
View SolutionA ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take g=10ms−2.
View SolutionA ball is thrown vertically upwards with a velcotiy of 20ms−1 from the top of a multi-storey building. The height of the point fromwher the ball is thrown if 25m from the ground. (a) How high the ball will rise ? And (b) how long will it be before the ball hits the ground ? Take. g=10ms−2.
View SolutionA ball is thrown vertically upwards with a velcotiy of 20 ms^(-1) from the top of a multi-storey building. The height of the point fromwher the ball is thrown if 25m from the ground. (a) How high the ball will rise ? And (b) how long will it be before the ball hits the ground ? Take. g=10 ms^(-2) .
View Solution
