Obtain equations of motion for constant acceleration using method of calculus.Solution in Gujrati
By definition
a=dυdt
dυ=adt
Integrating both sides
∫υυ0dυ=∫t0adt
=a∫t0dt (a is constant)
υ−υ0=at
υ=υ0+at
Further, υ=dxdt
dx=υdt
Integrating both sides
∫xx0dx=∫t0υdt
=∫t0(υ0+at)dt
x−x0=υ0t+12at2
x=x0+υ0t+12at2
We can write
a=dυdt=dυdxdxdt=υdυdx
or υdυ=adx
Integrating both sides,
∫υυ0υdυ=∫xx0adx
υ2−υ202=a(x−x0)
υ2=υ20+2a(x−x0)
The advantage of this method is that it can be used for motion with non-uniform acceleration also. Now, we shall use these equations to some important cases. t
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NCERT GUJARATICHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISES
23 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT GUJARATICHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES
5 Videos
- MOTION IN A PLANEBOOK - NCERT GUJARATICHAPTER - MOTION IN A PLANEEXERCISE - EXCERCISES
30 Videos
- OSCILLATIONSBOOK - NCERT GUJARATICHAPTER - OSCILLATIONSEXERCISE - Additional Exercises
6 Videos
Similar Questions
The angle of elevation of a bird sitting on top of a tree as seen from the point at a distance of 20m from the base of the tree is 60∘. Then, the height of the tree is ……..m
View SolutionA boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can equal to 49 ms-1. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of 5 ms−1 and the boy again throws the ball up with the maximum speed he can, how long goes the ball take to return to his hands ?
View SolutionState , for each of the following physical quantities , if it is a scalar or a vector : volume , mass , speed , acceleration , density , number of moles , velocity , angular frequency , displacement , angular velocity .
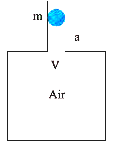
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
View SolutionDerivations Of Equation Of Motion By Calculus Method
View SolutionDeduce the equations of unifromly accelerated motion in one dimension by following calculus method.
View SolutionDerive equations of uniformly acceleration motion by calculus method.
View SolutionDerive equations of uniformly acceleration motion by calculus method.
View SolutionObtain equations of motion for constant a acceleration using the method of calculus.
View SolutionMotion With Constant Acceleration|Equation Of Motion
View SolutionDerive the equations of motion for an object in uniformly accelerated motion in one dimension using calculus.
View SolutionObtain equations of motion for constant acceleration using method of calculus.
View SolutionObtain equations of motion for constant acceleration using method of calculus.
View SolutionDerive the equations of uniformaly accelerated motion by graphical method.
View SolutionObtain equations of motion for constant acceleration using method of calculus.
View Solution
